Menu Close

tanA-1-cotA-cotA-1-tanA-secA-cosecA-1-Please-prove-it-for-me-

Tinku Tara 0 Comments
Pin




Question Number 122118 by AbdullahMohammadNurusSafa last updated on 14/Nov/20
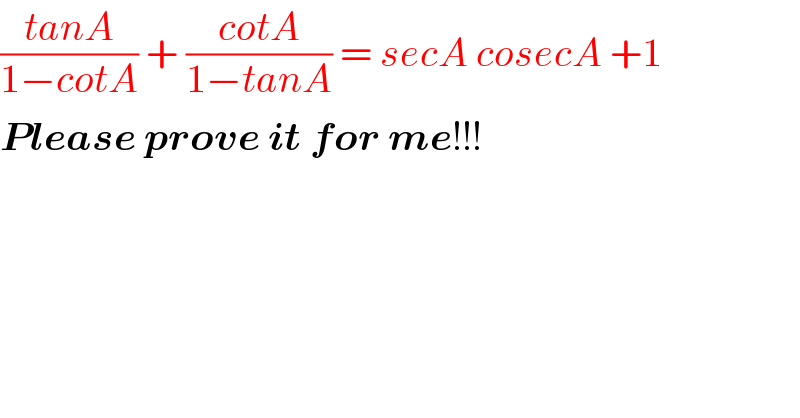
((tanA)/(1−cotA)) + ((cotA)/(1−tanA)) = secA cosecA +1 Please prove it for me!!!
$$\frac{{tanA}}{\mathrm{1}−{cotA}}\:+\:\frac{{cotA}}{\mathrm{1}−{tanA}}\:=\:{secA}\:{cosecA}\:+\mathrm{1} \\ $$$$\boldsymbol{{Please}}\:\boldsymbol{{prove}}\:\boldsymbol{{it}}\:\boldsymbol{{for}}\:\boldsymbol{{me}}!!! \\ $$
Answered by MJS_new last updated on 14/Nov/20
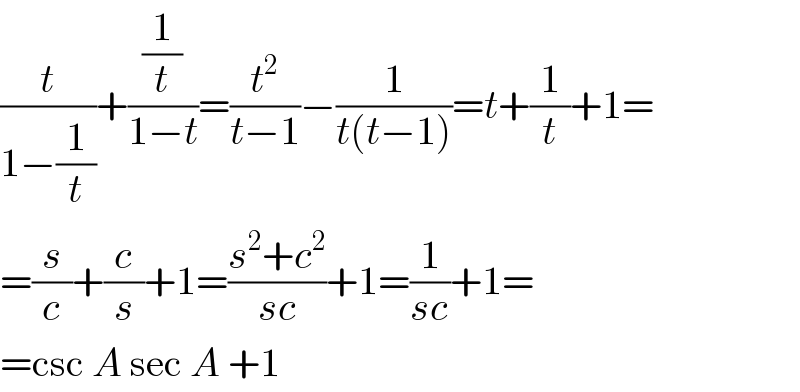
(t/(1−(1/t)))+((1/t)/(1−t))=(t^2 /(t−1))−(1/(t(t−1)))=t+(1/t)+1= =(s/c)+(c/s)+1=((s^2 +c^2 )/(sc))+1=(1/(sc))+1= =csc A sec A +1
$$\frac{{t}}{\mathrm{1}−\frac{\mathrm{1}}{{t}}}+\frac{\frac{\mathrm{1}}{{t}}}{\mathrm{1}−{t}}=\frac{{t}^{\mathrm{2}} }{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}\left({t}−\mathrm{1}\right)}={t}+\frac{\mathrm{1}}{{t}}+\mathrm{1}= \\ $$$$=\frac{{s}}{{c}}+\frac{{c}}{{s}}+\mathrm{1}=\frac{{s}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{sc}}+\mathrm{1}=\frac{\mathrm{1}}{{sc}}+\mathrm{1}= \\ $$$$=\mathrm{csc}\:{A}\:\mathrm{sec}\:{A}\:+\mathrm{1} \\ $$
Answered by bemath last updated on 14/Nov/20
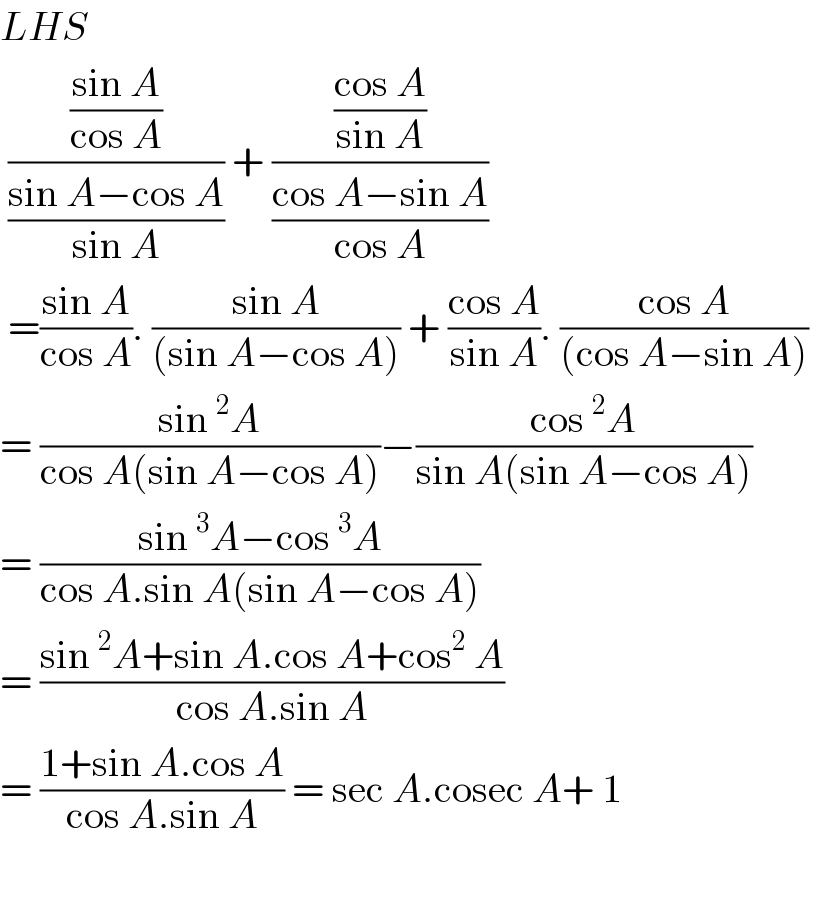
LHS (((sin A)/(cos A))/((sin A−cos A)/(sin A))) + (((cos A)/(sin A))/((cos A−sin A)/(cos A))) =((sin A)/(cos A)). ((sin A)/((sin A−cos A))) + ((cos A)/(sin A)). ((cos A)/((cos A−sin A))) = ((sin^2 A)/(cos A(sin A−cos A)))−((cos^2 A)/(sin A(sin A−cos A))) = ((sin^3 A−cos^3 A)/(cos A.sin A(sin A−cos A))) = ((sin^2 A+sin A.cos A+cos^2 A)/(cos A.sin A)) = ((1+sin A.cos A)/(cos A.sin A)) = sec A.cosec A+ 1
$${LHS} \\ $$$$\:\frac{\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}}{\frac{\mathrm{sin}\:{A}−\mathrm{cos}\:{A}}{\mathrm{sin}\:{A}}}\:+\:\frac{\frac{\mathrm{cos}\:{A}}{\mathrm{sin}\:{A}}}{\frac{\mathrm{cos}\:{A}−\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}} \\ $$$$\:=\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}.\:\frac{\mathrm{sin}\:{A}}{\left(\mathrm{sin}\:{A}−\mathrm{cos}\:{A}\right)}\:+\:\frac{\mathrm{cos}\:{A}}{\mathrm{sin}\:{A}}.\:\frac{\mathrm{cos}\:{A}}{\left(\mathrm{cos}\:{A}−\mathrm{sin}\:{A}\right)}\: \\ $$$$=\:\frac{\mathrm{sin}\:^{\mathrm{2}} {A}}{\mathrm{cos}\:{A}\left(\mathrm{sin}\:{A}−\mathrm{cos}\:{A}\right)}−\frac{\mathrm{cos}\:^{\mathrm{2}} {A}}{\mathrm{sin}\:{A}\left(\mathrm{sin}\:{A}−\mathrm{cos}\:{A}\right)} \\ $$$$=\:\frac{\mathrm{sin}\:^{\mathrm{3}} {A}−\mathrm{cos}\:^{\mathrm{3}} {A}}{\mathrm{cos}\:{A}.\mathrm{sin}\:{A}\left(\mathrm{sin}\:{A}−\mathrm{cos}\:{A}\right)} \\ $$$$=\:\frac{\mathrm{sin}\:^{\mathrm{2}} {A}+\mathrm{sin}\:{A}.\mathrm{cos}\:{A}+\mathrm{cos}^{\mathrm{2}} \:{A}}{\mathrm{cos}\:{A}.\mathrm{sin}\:{A}} \\ $$$$=\:\frac{\mathrm{1}+\mathrm{sin}\:{A}.\mathrm{cos}\:{A}}{\mathrm{cos}\:{A}.\mathrm{sin}\:{A}}\:=\:\mathrm{sec}\:{A}.\mathrm{cosec}\:{A}+\:\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *