Question Number 20686 by NECx last updated on 31/Aug/17
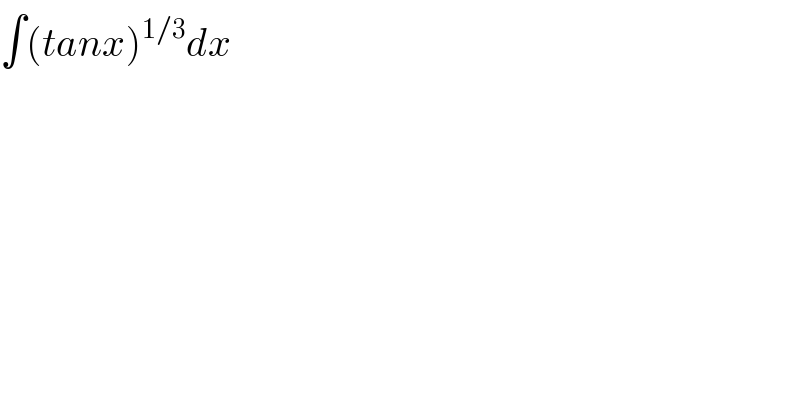
$$\int\left({tanx}\right)^{\mathrm{1}/\mathrm{3}} {dx} \\ $$
Commented by NECx last updated on 01/Sep/17

$${please}\:{help} \\ $$
Answered by ajfour last updated on 01/Sep/17
![let tan x= (1/t^3 ) ⇒ sec^2 xdx=((−3dt)/t^4 ) I=∫(tan x)^(1/3) dx = ∫(1/t)×((−3dt)/(t^4 (1+(1/t^6 )))) =−3∫((tdt)/(1+t^6 )) =−(3/2)∫((2tdt)/(1+(t^2 )^3 )) let t^2 =z I=−(3/2)∫(dz/(1+z^3 )) =−(3/2)∫(dz/((1+z)(z^2 −z+1))) =−(3/2)∫[((1/3)/(1+z))+((−1/3x+2/3)/(z^2 −z+1))]dz =−(1/2)ln ∣1+z∣+(1/4)∫((2z−4)/(z^2 −z+1))dz =−(1/2)ln ∣1+z∣+(1/4)∫((2z−1)/(z^2 −z+1))dz −(3/4)∫(dz/((z−(1/2))^2 +(((√3)/2))^2 )) =−(1/2)ln ∣1+z∣+(1/4)ln ∣z^2 −z+1∣ −(3/4)((2/( (√3))))tan^(−1) (((2z−1)/( (√3)))) +C where z=t^2 = (tan x)^(−2/3) .](https://www.tinkutara.com/question/Q20710.png)
$${let}\:\:\mathrm{tan}\:{x}=\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:\:\:\:\Rightarrow\:\:\mathrm{sec}\:^{\mathrm{2}} {xdx}=\frac{−\mathrm{3}{dt}}{{t}^{\mathrm{4}} } \\ $$$$\:\boldsymbol{{I}}=\int\left(\mathrm{tan}\:{x}\right)^{\mathrm{1}/\mathrm{3}} {dx}\:=\:\int\frac{\mathrm{1}}{{t}}×\frac{−\mathrm{3}{dt}}{{t}^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{6}} }\right)} \\ $$$$\:\:\:=−\mathrm{3}\int\frac{{tdt}}{\mathrm{1}+{t}^{\mathrm{6}} }\:\:\:=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}{tdt}}{\mathrm{1}+\left({t}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${let}\:\:{t}^{\mathrm{2}} ={z}\: \\ $$$$\boldsymbol{{I}}=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{3}} }\:=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{\left(\mathrm{1}+{z}\right)\left({z}^{\mathrm{2}} −{z}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{3}}{\mathrm{2}}\int\left[\frac{\mathrm{1}/\mathrm{3}}{\mathrm{1}+{z}}+\frac{−\mathrm{1}/\mathrm{3}{x}+\mathrm{2}/\mathrm{3}}{{z}^{\mathrm{2}} −{z}+\mathrm{1}}\right]{dz} \\ $$$$\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+{z}\mid+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{z}−\mathrm{4}}{{z}^{\mathrm{2}} −{z}+\mathrm{1}}{dz} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+{z}\mid+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{z}−\mathrm{1}}{{z}^{\mathrm{2}} −{z}+\mathrm{1}}{dz} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{3}}{\mathrm{4}}\int\frac{{dz}}{\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+{z}\mid+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid{z}^{\mathrm{2}} −{z}+\mathrm{1}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{z}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{C} \\ $$$$\:\:\:{where}\:\:\:\:\:{z}={t}^{\mathrm{2}} \:=\:\left(\mathrm{tan}\:{x}\right)^{−\mathrm{2}/\mathrm{3}} \:. \\ $$
Answered by $@ty@m last updated on 01/Sep/17

$${Alternative}\:{method}: \\ $$$${Let}\:{tanx}={w}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow{sec}^{\mathrm{2}} {xdx}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{w}}{dw} \\ $$$$\Rightarrow{dx}=\frac{\mathrm{3}}{\mathrm{2}}.\frac{\sqrt{{w}}{dw}}{\mathrm{1}+{w}^{\mathrm{3}} } \\ $$$$\therefore\int\left({tanx}\right)^{\mathrm{1}/\mathrm{3}} {dx}=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{w}}{\mathrm{1}+{w}^{\mathrm{3}} }{dw} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{w}}{\left(\mathrm{1}+{w}\right)\left(\mathrm{1}−{w}+{w}^{\mathrm{2}} \right)}{dw} \\ $$$${Let}\:\frac{{w}}{\left(\mathrm{1}+{w}\right)\left(\mathrm{1}−{w}+{w}^{\mathrm{2}} \right)}=\frac{{A}}{\mathrm{1}+{w}}+\frac{{Bw}+{C}}{\mathrm{1}−{w}+{w}^{\mathrm{2}} } \\ $$$$\Rightarrow{A}\left(\mathrm{1}−{w}+{w}^{\mathrm{2}} \right)+\left({Bw}+{C}\right)\left(\mathrm{1}+{w}\right)\equiv{w} \\ $$$$\Rightarrow{A}+{C}=\mathrm{0},\:−{A}+{B}+{C}=\mathrm{1},\:{A}+{B}=\mathrm{0} \\ $$$$\Rightarrow{B}={C}=\:\frac{\mathrm{1}}{\mathrm{3}},\:{A}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$${now}\:{proceed}\:{similar}\:{to}\:{above}\:{solution}. \\ $$
Commented by NECx last updated on 01/Sep/17
$${wow}….\:{i}\:{really}\:{appreciate}\:{this}. \\ $$
