Question Number 64471 by mmkkmm000m last updated on 18/Jul/19
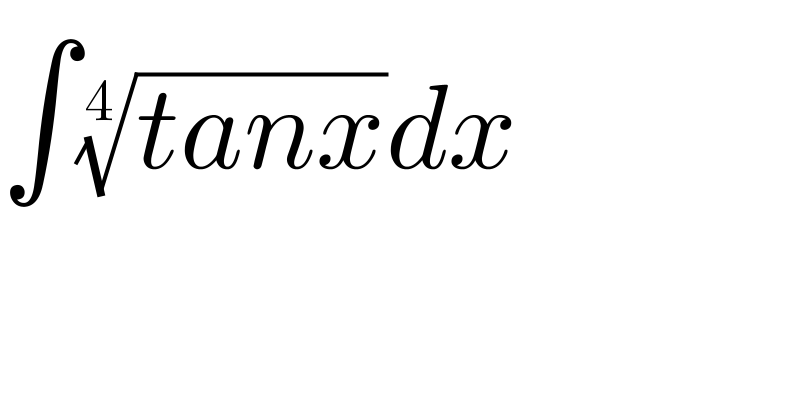
$$\int\sqrt[{\mathrm{4}}]{{tanx}}{dx} \\ $$
Answered by MJS last updated on 18/Jul/19
![∫((tan x))^(1/4) dx= [t=((tan x))^(1/4) → dx=4((tan^3 x))^(1/4) cos^2 x dt] =4∫(t^4 /(t^8 +1))dt this can be solved but I have no time...](https://www.tinkutara.com/question/Q64496.png)
$$\int\sqrt[{\mathrm{4}}]{\mathrm{tan}\:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{4}}]{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{4}\sqrt[{\mathrm{4}}]{\mathrm{tan}^{\mathrm{3}} \:{x}}\:\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\mathrm{4}\int\frac{{t}^{\mathrm{4}} }{{t}^{\mathrm{8}} +\mathrm{1}}{dt} \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{but}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}… \\ $$
Commented by MJS last updated on 18/Jul/19

$$\mathrm{let}\:{a}=\sqrt{\mathrm{2}}\:\:\:{b}=\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\:\:\:{c}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$$\frac{\mathrm{4}{t}^{\mathrm{4}} }{{t}^{\mathrm{8}} +\mathrm{1}}=\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\frac{−{a}}{\mathrm{4}\left({t}^{\mathrm{2}} −{bt}+\mathrm{1}\right)}−\frac{{c}\left(\mathrm{2}{t}−{b}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −{bt}+\mathrm{1}\right)} \\ $$$$\frac{−{a}}{\mathrm{4}\left({t}^{\mathrm{2}} +{bt}+\mathrm{1}\right)}+\frac{{c}\left(\mathrm{2}{t}+{b}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} +{bt}+\mathrm{1}\right)} \\ $$$$\frac{{a}}{\mathrm{4}\left({t}^{\mathrm{2}} −{ct}+\mathrm{1}\right)}+\frac{{b}\left(\mathrm{2}{t}−{c}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −{ct}+\mathrm{1}\right)} \\ $$$$\frac{{a}}{\mathrm{4}\left({t}^{\mathrm{2}} +{ct}+\mathrm{1}\right)}−\frac{{b}\left(\mathrm{2}{t}+{c}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} +{ct}+\mathrm{1}\right)} \\ $$$$\mathrm{their}\:\mathrm{integrals}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
