Question Number 100097 by Dwaipayan Shikari last updated on 24/Jun/20
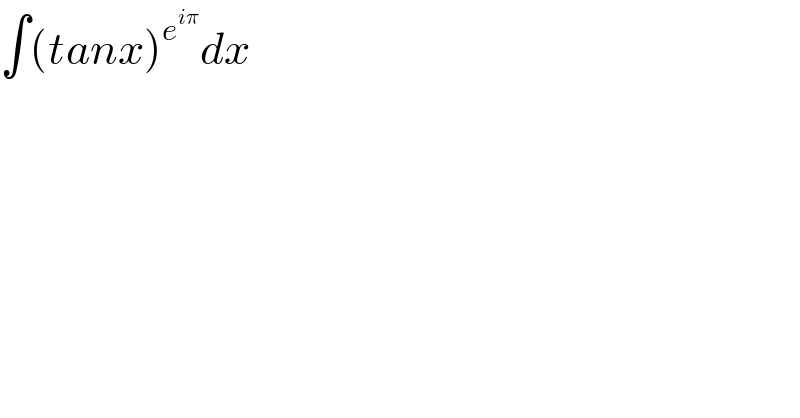
$$\int\left({tanx}\right)^{{e}^{{i}\pi} } {dx} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20
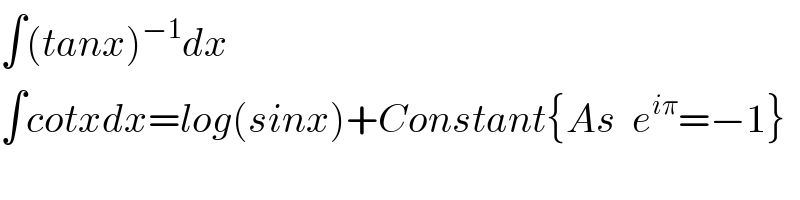
$$\int\left({tanx}\right)^{−\mathrm{1}} {dx} \\ $$$$\int{cotxdx}={log}\left({sinx}\right)+{Constant}\left\{{As}\:\:{e}^{{i}\pi} =−\mathrm{1}\right\} \\ $$
