Menu Close

Ten-balls-were-manufactured-nine-of-them-have-the-same-mass-while-just-one-of-them-has-a-slightly-higher-or-slightly-lower-mass-Given-is-just-a-beam-balance-and-no-weights-comparing-the-masses-of

Tinku Tara 0 Comments
Pin




Question Number 16450 by ajfour last updated on 22/Jun/17
Ten balls were manufactured, nine of them have the same mass, while just one of them has a slightly higher or slightly lower mass. Given is just a beam balance and no weights. comparing the masses of balls only, with the help of the balance , and in just 3 weighings explain how to judge which is the defective one and whether it is heavier or lighter than the rest (as the case may be).
$${Ten}\:{balls}\:{were}\:{manufactured}, \\ $$$$\:{nine}\:{of}\:{them}\:{have}\:{the}\:{same} \\ $$$${mass},\:{while}\:{just}\:{one}\:{of}\:{them} \\ $$$${has}\:{a}\:{slightly}\:{higher}\:{or}\:{slightly} \\ $$$${lower}\:{mass}.\:{Given}\:{is}\:{just}\:{a}\:{beam} \\ $$$${balance}\:{and}\:{no}\:{weights}.\:{comparing} \\ $$$${the}\:{masses}\:{of}\:{balls}\:{only},\:{with}\:{the} \\ $$$${help}\:{of}\:{the}\:{balance}\:,\:{and}\:{in}\:{just} \\ $$$$\mathrm{3}\:{weighings}\:{explain}\:{how}\:{to}\:{judge} \\ $$$${which}\:{is}\:{the}\:{defective}\:{one}\:{and} \\ $$$${whether}\:{it}\:{is}\:{heavier}\:{or}\:{lighter} \\ $$$${than}\:{the}\:{rest}\:\left({as}\:{the}\:{case}\:{may}\:{be}\right). \\ $$
Commented by prakash jain last updated on 22/Jun/17
10 balls=b_1 ,...,b_(10) set A=b_1 ,b_2 ,b_3 set B=b_4 ,b_5 ,b_6 set C=b_7 ,b_8 ,b_9 2 weighs compare A&B and A&C case 1: A=B=C b_(10) is fault. measure b_(10) with b_1 to find out if b_(10) is heavier to lighter. case 2: one of group is unequal at we know the defective set and whether it is heavier to lighter than the other. Let us say set is A. compare b_1 and b_2 if equal b_3 is defectivd if equal b_3 is defectivd if not equal the heavier or lighter ball is defective. (we already identified the nature of defecr)
$$\mathrm{10}\:\mathrm{balls}={b}_{\mathrm{1}} ,…,{b}_{\mathrm{10}} \\ $$$${set}\:\mathrm{A}={b}_{\mathrm{1}} ,{b}_{\mathrm{2}} ,{b}_{\mathrm{3}} \\ $$$${set}\:{B}={b}_{\mathrm{4}} ,{b}_{\mathrm{5}} ,{b}_{\mathrm{6}} \\ $$$${set}\:{C}={b}_{\mathrm{7}} ,{b}_{\mathrm{8}} ,{b}_{\mathrm{9}} \\ $$$$\mathrm{2}\:\mathrm{weighs}\:\mathrm{compare}\:\mathrm{A\&B}\:\mathrm{and}\:\mathrm{A\&C}\: \\ $$$$\mathrm{case}\:\mathrm{1}:\:\mathrm{A}=\mathrm{B}=\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:{b}_{\mathrm{10}} \:\mathrm{is}\:\mathrm{fault}. \\ $$$$\:\:\:\:\:\:\:\:\mathrm{measure}\:{b}_{\mathrm{10}} \:\mathrm{with}\:{b}_{\mathrm{1}} \:\mathrm{to}\:\mathrm{find}\:\mathrm{out} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{if}\:{b}_{\mathrm{10}} \:\mathrm{is}\:\mathrm{heavier}\:\mathrm{to}\:\mathrm{lighter}. \\ $$$$\mathrm{case}\:\mathrm{2}:\:\mathrm{one}\:\mathrm{of}\:\mathrm{group}\:\mathrm{is}\:\mathrm{unequal} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{at}\:\mathrm{we}\:\mathrm{know}\:\mathrm{the}\:\mathrm{defective}\:\mathrm{set} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{and}\:\mathrm{whether}\:\mathrm{it}\:\mathrm{is}\:\mathrm{heavier}\:\mathrm{to}\:\mathrm{lighter} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{than}\:\mathrm{the}\:\mathrm{other}.\:\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{set}\:\mathrm{is}\:\mathrm{A}. \\ $$$$\:\:\:\:\:\:\:\:\mathrm{compare}\:{b}_{\mathrm{1}} \:\mathrm{and}\:{b}_{\mathrm{2}} \:\mathrm{if}\:\mathrm{equal}\:{b}_{\mathrm{3}} \:\mathrm{is}\:\mathrm{defectivd} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{equal}\:{b}_{\mathrm{3}} \:\mathrm{is}\:\mathrm{defectivd} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{not}\:\mathrm{equal}\:\mathrm{the}\:\mathrm{heavier}\:\mathrm{or}\:\mathrm{lighter} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{ball}\:\mathrm{is}\:\mathrm{defective}.\:\left(\mathrm{we}\:\mathrm{already}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{identified}\:\mathrm{the}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{defecr}\right) \\ $$
Commented by prakash jain last updated on 22/Jun/17
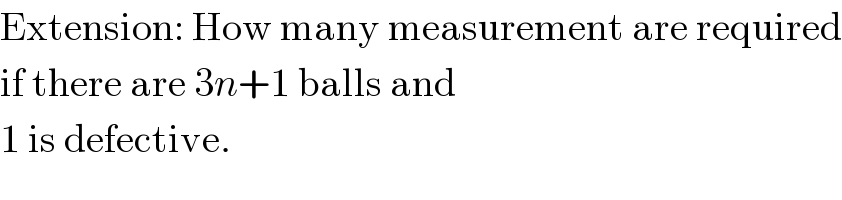
Extension: How many measurement are required if there are 3n+1 balls and 1 is defective.
$$\mathrm{Extension}:\:\mathrm{How}\:\mathrm{many}\:\mathrm{measurement}\:\mathrm{are}\:\mathrm{required} \\ $$$$\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{3}{n}+\mathrm{1}\:\mathrm{balls}\:\mathrm{and} \\ $$$$\mathrm{1}\:\mathrm{is}\:\mathrm{defective}. \\ $$
Commented by ajfour last updated on 23/Jun/17
Great solving sir, good noticing ability. Thanks.
$$\:{Great}\:{solving}\:{sir},\:{good}\:{noticing} \\ $$$$\:{ability}.\:{Thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *