Question Number 119636 by I want to learn more last updated on 25/Oct/20

$$\mathrm{Test}\:\mathrm{wheather}\:\mathrm{convergent} \\ $$$$\:\:\:\underset{\mathrm{n}\:\:=\:\:\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{3n}\:\:−\:\:\mathrm{1}}{\mathrm{7}^{\mathrm{n}} \:\:+\:\:\mathrm{2n}} \\ $$
Answered by 1549442205PVT last updated on 26/Oct/20
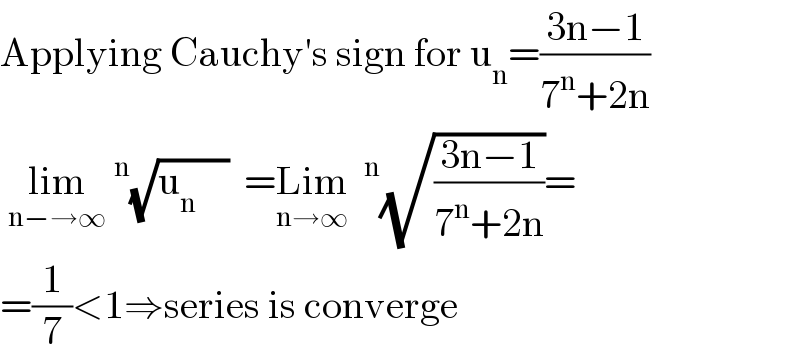
$$\mathrm{Applying}\:\mathrm{Cauchy}'\mathrm{s}\:\mathrm{sign}\:\mathrm{for}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3n}−\mathrm{1}}{\mathrm{7}^{\mathrm{n}} +\mathrm{2n}} \\ $$$$\:\underset{\mathrm{n}−\rightarrow\infty} {\mathrm{lim}}\:^{\mathrm{n}} \sqrt{\mathrm{u}_{\mathrm{n}} \:\:\:\:}\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{Lim}}\:\:^{\mathrm{n}} \sqrt{\frac{\mathrm{3n}−\mathrm{1}}{\mathrm{7}^{\mathrm{n}} +\mathrm{2n}}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}<\mathrm{1}\Rightarrow\mathrm{series}\:\mathrm{is}\:\mathrm{converge} \\ $$
Commented by I want to learn more last updated on 27/Oct/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by 1549442205PVT last updated on 27/Oct/20
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
