Question Number 62982 by ANTARES VY last updated on 27/Jun/19
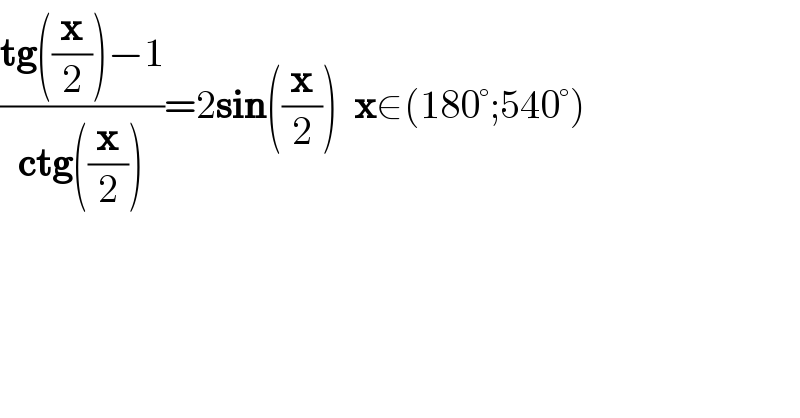
$$\frac{\boldsymbol{\mathrm{tg}}\left(\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)−\mathrm{1}}{\boldsymbol{\mathrm{ctg}}\left(\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)}=\mathrm{2}\boldsymbol{\mathrm{sin}}\left(\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)\:\:\boldsymbol{\mathrm{x}}\in\left(\mathrm{180}°;\mathrm{540}°\right) \\ $$$$ \\ $$
Answered by MJS last updated on 27/Jun/19
![(1/(cot))=tan tan^2 (x/2) −tan (x/2) −2sin (x/2) =0 let x=4arctan t ((−2t(t^4 −2t^3 −4t^2 −2t+3))/((t−1)^3 (t+1)^2 (t^2 +1)))=0 ⇒ t_1 =0 t^4 −2t^3 −4t^3 −2t+3=0 no “nice” solution t_2 ≈.607081 t_3 ≈3.30877 t_(4, 5) ∉R ⇒ x_1 =360°×z x_2 ≈125.04°+720°×z x_3 ≈292.74°+720°×z x∈[180°; 540°] ⇒ x≈292.74°∨x≈360°](https://www.tinkutara.com/question/Q63019.png)
$$\frac{\mathrm{1}}{\mathrm{cot}}=\mathrm{tan} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\:−\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:−\mathrm{2sin}\:\frac{{x}}{\mathrm{2}}\:=\mathrm{0} \\ $$$$\mathrm{let}\:{x}=\mathrm{4arctan}\:{t} \\ $$$$\frac{−\mathrm{2}{t}\left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{3}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)}=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} =\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}{t}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{no}\:“\mathrm{nice}''\:\mathrm{solution} \\ $$$${t}_{\mathrm{2}} \approx.\mathrm{607081} \\ $$$${t}_{\mathrm{3}} \approx\mathrm{3}.\mathrm{30877} \\ $$$${t}_{\mathrm{4},\:\mathrm{5}} \notin\mathbb{R} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\mathrm{360}°×{z} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{125}.\mathrm{04}°+\mathrm{720}°×{z} \\ $$$${x}_{\mathrm{3}} \approx\mathrm{292}.\mathrm{74}°+\mathrm{720}°×{z} \\ $$$${x}\in\left[\mathrm{180}°;\:\mathrm{540}°\right]\:\Rightarrow\:{x}\approx\mathrm{292}.\mathrm{74}°\vee{x}\approx\mathrm{360}° \\ $$
