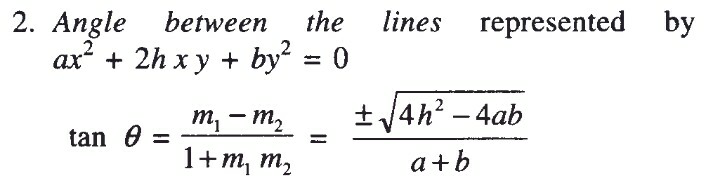Question Number 21341 by gopikrishnan005@gmail.com last updated on 21/Sep/17

$${the}\:{angle}\:{between}\:{the}\:{straight}\:{lines}\:{x}^{\mathrm{2}} +\mathrm{4}{xy}+\mathrm{3}{y}^{\mathrm{2}} =\mathrm{0}\:{is} \\ $$
Answered by mrW1 last updated on 21/Sep/17
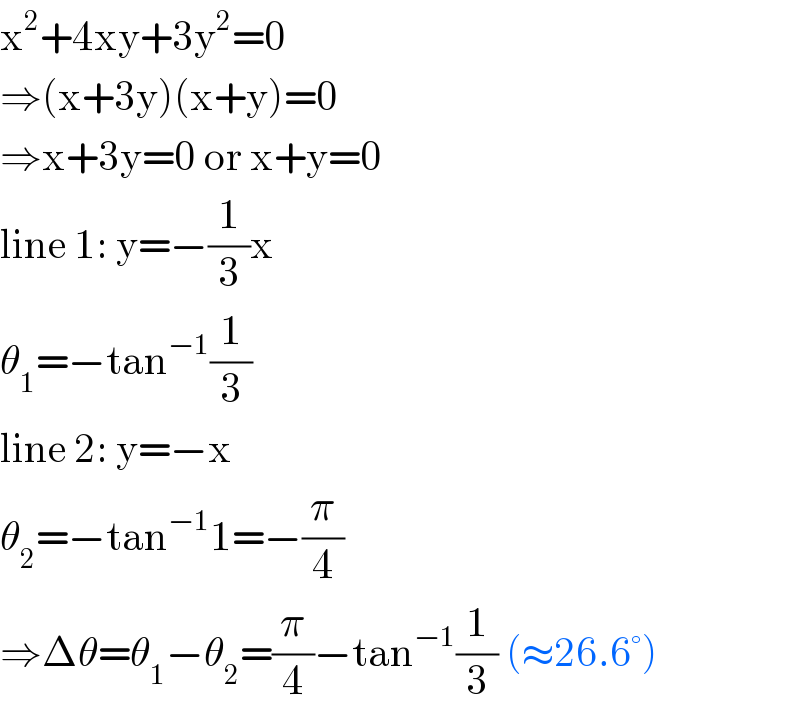
$$\mathrm{x}^{\mathrm{2}} +\mathrm{4xy}+\mathrm{3y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{3y}\right)\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{3y}=\mathrm{0}\:\mathrm{or}\:\mathrm{x}+\mathrm{y}=\mathrm{0} \\ $$$$\mathrm{line}\:\mathrm{1}:\:\mathrm{y}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x} \\ $$$$\theta_{\mathrm{1}} =−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{line}\:\mathrm{2}:\:\mathrm{y}=−\mathrm{x} \\ $$$$\theta_{\mathrm{2}} =−\mathrm{tan}^{−\mathrm{1}} \mathrm{1}=−\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\Delta\theta=\theta_{\mathrm{1}} −\theta_{\mathrm{2}} =\frac{\pi}{\mathrm{4}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\:\left(\approx\mathrm{26}.\mathrm{6}°\right) \\ $$
Answered by $@ty@m last updated on 22/Sep/17