The-arc-of-parabola-y-x-2-9-in-0-lt-x-lt-3-is-revolved-about-the-line-y-c-and-0-lt-c-lt-9-to-generate-a-solid-Find-the-value-of-c-that-minimizes-the-volume-of-the-solid-

FacebookTweetPin

Question Number 163223 by ZiYangLee last updated on 05/Jan/22

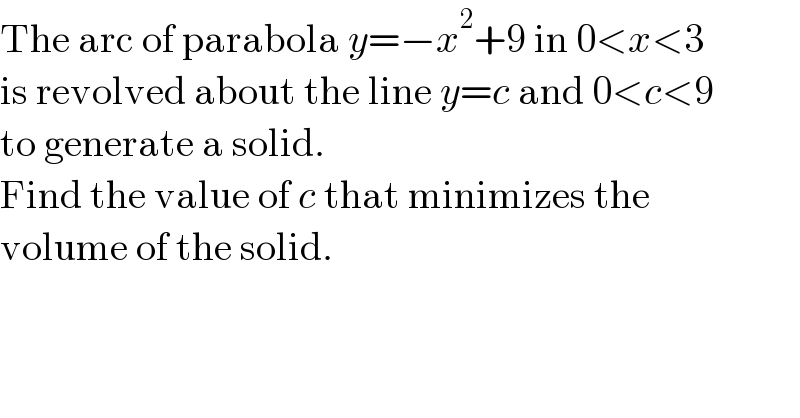
$$\mathrm{The}\mathrm{arc}\mathrm{of}\mathrm{parabola}y=-x^2+9\mathrm{in}0<x<3$$$$\mathrm{is}\mathrm{revolved}\mathrm{about}\mathrm{the}\mathrm{line}y=c\mathrm{and}0<c<9$$$$\mathrm{to}\mathrm{generate}\mathrm{a}\mathrm{solid}.$$$$\mathrm{Find}\mathrm{the}\mathrm{value}\mathrm{of}c\mathrm{that}\mathrm{minimizes}\mathrm{the}$$$$\mathrm{volume}\mathrm{of}\mathrm{the}\mathrm{solid}.$$

Answered by TheSupreme last updated on 05/Jan/22

$$f\left(x\right)=-x^2+9-c$$$$V=2\pi {\int }_{-3}^{3}f{\left(x\right)}^{2}dx=2\pi {\int }_{-3}^3{(9-c)}^2+x^4-2x^2(9-c)dx=$$$$=2\pi [6{(9-c)}^2+2\frac{3^5}{5}-2\frac{3^3}{3}(9-c)]$$$$\frac{\partial V}{\partial c}=2\pi [-12(9-c)+12]=0$$$$2\pi [-12\cdot 9+12c+12]=0$$$$12c=12\cdot 8$$$$c=8$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin