Question Number 89661 by Mr.Panoply last updated on 18/Apr/20
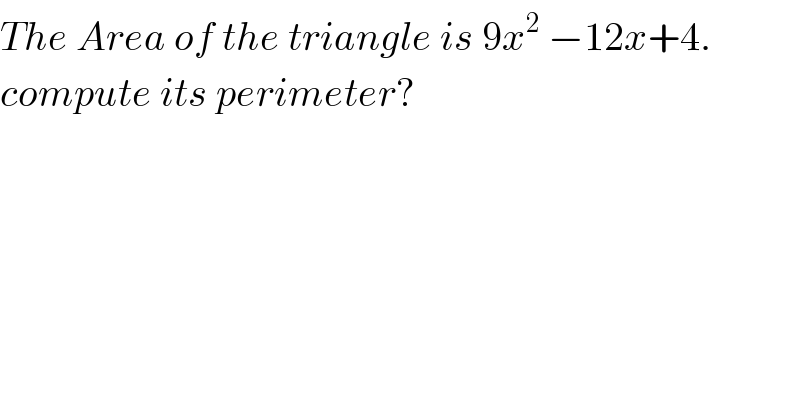
$${The}\:{Area}\:{of}\:{the}\:{triangle}\:{is}\:\mathrm{9}{x}^{\mathrm{2}} \:−\mathrm{12}{x}+\mathrm{4}. \\ $$$${compute}\:{its}\:{perimeter}? \\ $$
Commented by mr W last updated on 19/Apr/20
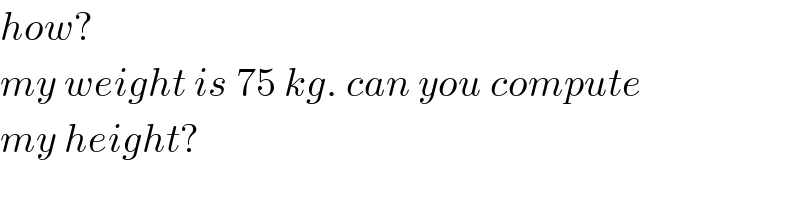
$${how}? \\ $$$${my}\:{weight}\:{is}\:\mathrm{75}\:{kg}.\:{can}\:{you}\:{compute} \\ $$$${my}\:{height}? \\ $$
Commented by Kunal12588 last updated on 18/Apr/20
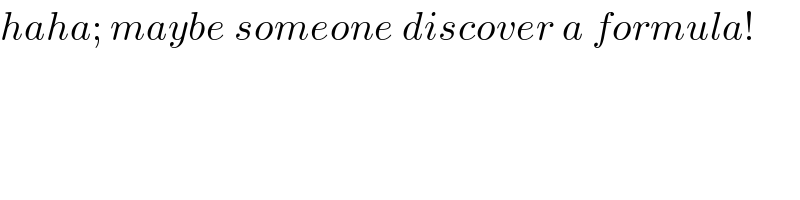
$${haha};\:{maybe}\:{someone}\:{discover}\:{a}\:{formula}! \\ $$
Commented by MJS last updated on 18/Apr/20
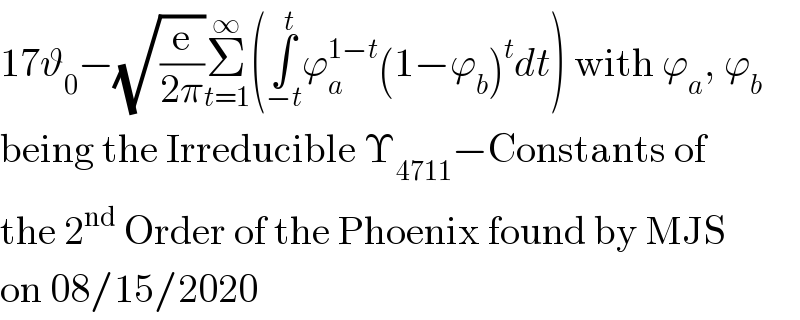
$$\mathrm{17}\vartheta_{\mathrm{0}} −\sqrt{\frac{\mathrm{e}}{\mathrm{2}\pi}}\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\underset{−{t}} {\overset{{t}} {\int}}\varphi_{{a}} ^{\mathrm{1}−{t}} \left(\mathrm{1}−\varphi_{{b}} \right)^{{t}} {dt}\right)\:\mathrm{with}\:\varphi_{{a}} ,\:\varphi_{{b}} \\ $$$$\mathrm{being}\:\mathrm{the}\:\mathrm{Irreducible}\:\Upsilon_{\mathrm{4711}} −\mathrm{Constants}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{Order}\:\mathrm{of}\:\mathrm{the}\:\mathrm{Phoenix}\:\mathrm{found}\:\mathrm{by}\:\mathrm{MJS} \\ $$$$\mathrm{on}\:\mathrm{08}/\mathrm{15}/\mathrm{2020} \\ $$
