Question Number 127119 by liberty last updated on 27/Dec/20

$${The}\:{barometric}\:{pressure}\:{p}\:{at}\:{an}\:{altitude} \\ $$$${of}\:{h}\:{miles}\:{above}\:{sea}\:{level}\:{satisfies}\:{the} \\ $$$${differential}\:{equation}\:\frac{{dp}}{{dh}}\:=\:−\mathrm{0}.\mathrm{2}{p}\:. \\ $$$${If}\:{the}\:{pressure}\:{at}\:{sea}\:{level}\:{is}\:\mathrm{29}.\mathrm{92}\:{inches} \\ $$$${of}\:{mercury},\:{find}\:{the}\:{barometric}\: \\ $$$${preassure}\:{at}\:\mathrm{17},\mathrm{000}\:{ft}\: \\ $$$$\left({A}\right)\:\mathrm{56}.\mathrm{97}\:{in}\:\:\:\:\:\:\left({B}\right)\:\mathrm{15}.\mathrm{71}\:{in} \\ $$$$\left({C}\right)\:\mathrm{7}.\mathrm{86}\:{in}\:\:\:\:\:\:\:\:\:\:\left({D}\right)\:\mathrm{1}\:{in} \\ $$
Answered by benjo_mathlover last updated on 27/Dec/20
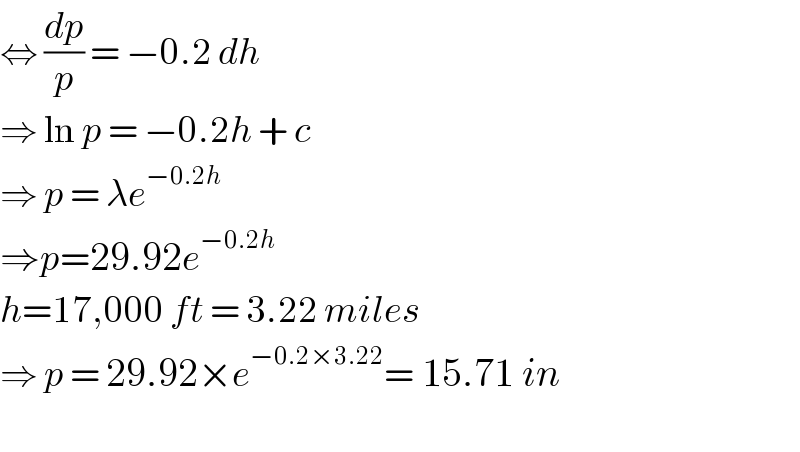
$$\Leftrightarrow\:\frac{{dp}}{{p}}\:=\:−\mathrm{0}.\mathrm{2}\:{dh} \\ $$$$\Rightarrow\:\mathrm{ln}\:{p}\:=\:−\mathrm{0}.\mathrm{2}{h}\:+\:{c}\: \\ $$$$\Rightarrow\:{p}\:=\:\lambda{e}^{−\mathrm{0}.\mathrm{2}{h}} \\ $$$$\Rightarrow{p}=\mathrm{29}.\mathrm{92}{e}^{−\mathrm{0}.\mathrm{2}{h}} \\ $$$${h}=\mathrm{17},\mathrm{000}\:{ft}\:=\:\mathrm{3}.\mathrm{22}\:{miles} \\ $$$$\Rightarrow\:{p}\:=\:\mathrm{29}.\mathrm{92}×{e}^{−\mathrm{0}.\mathrm{2}×\mathrm{3}.\mathrm{22}} =\:\mathrm{15}.\mathrm{71}\:{in} \\ $$$$ \\ $$
Commented by liberty last updated on 27/Dec/20
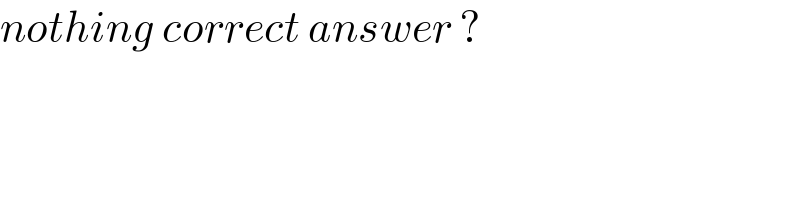
$${nothing}\:{correct}\:{answer}\:? \\ $$
Commented by mr W last updated on 27/Dec/20
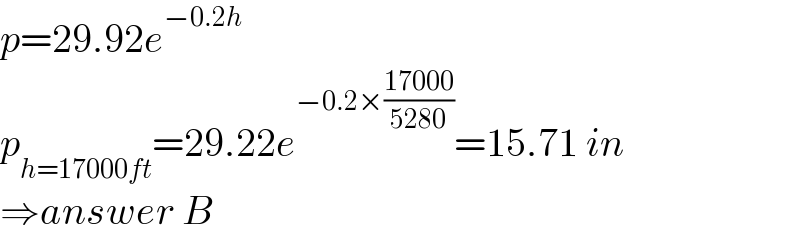
$${p}=\mathrm{29}.\mathrm{92}{e}^{−\mathrm{0}.\mathrm{2}{h}} \\ $$$${p}_{{h}=\mathrm{17000}{ft}} =\mathrm{29}.\mathrm{22}{e}^{−\mathrm{0}.\mathrm{2}×\frac{\mathrm{17000}}{\mathrm{5280}}} =\mathrm{15}.\mathrm{71}\:{in} \\ $$$$\Rightarrow{answer}\:{B} \\ $$
Commented by mr W last updated on 27/Dec/20
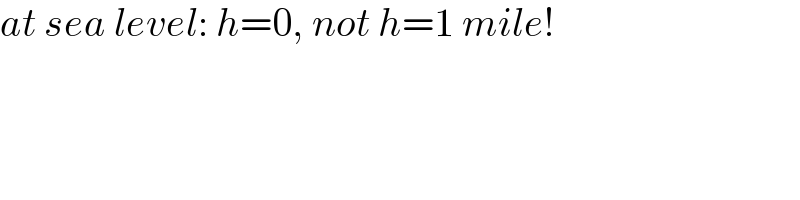
$${at}\:{sea}\:{level}:\:{h}=\mathrm{0},\:{not}\:{h}=\mathrm{1}\:{mile}! \\ $$
Commented by benjo_mathlover last updated on 27/Dec/20
$$\:\:{ooh}..\:{thank}\:{you}\:{sir} \\ $$
