Question Number 43005 by mondodotto@gmail.com last updated on 06/Sep/18
$$\mathrm{The}\:\mathrm{base}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{passes}\:\mathrm{through} \\ $$$$\mathrm{a}\:\mathrm{fixed}\:\mathrm{point}\:\mathrm{p}\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{and}\:\mathrm{its}\:\mathrm{sides} \\ $$$$\mathrm{are}\:\mathrm{respectively}\:\mathrm{bisected}\:\mathrm{at}\:\mathrm{right}\:\mathrm{angles}\: \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{line}\:\mathrm{x}+\mathrm{y}=\mathrm{0}\:\mathrm{and}\:\mathrm{x}=\mathrm{9y} \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{third}\:\mathrm{vartex}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}. \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{its}\:\mathrm{equation}. \\ $$
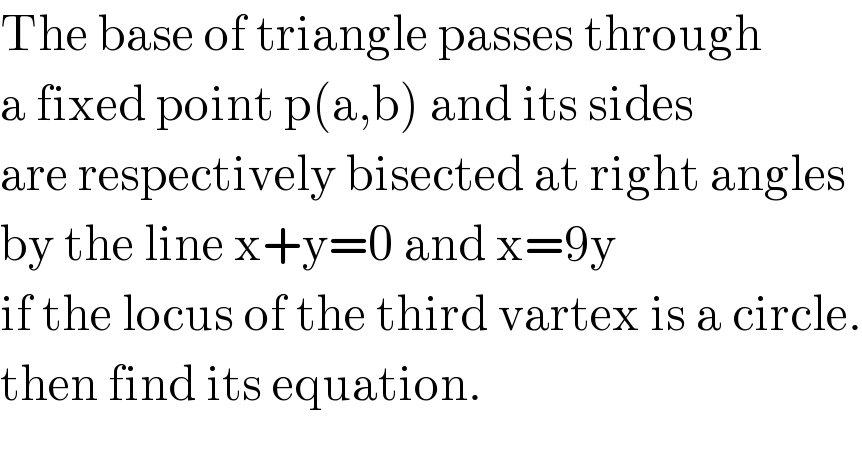
Commented by mondodotto@gmail.com last updated on 06/Sep/18
$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{this}\:\mathrm{problem} \\ $$
Commented by ajfour last updated on 06/Sep/18
Commented by ajfour last updated on 06/Sep/18
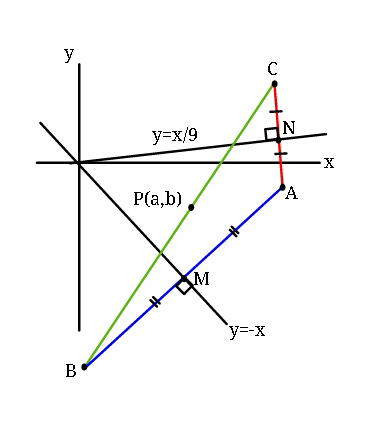
![let A(h,k) ⇒ B(−k, −h) let C(α, β) reflection of C in y=mx+c is α=h−((2m(c+mh−k))/(1+m^2 )) β = k+((2(c+mh−k))/(1+m^2 )) here we have y= (x/9) ⇒ m=(1/9) , c=0 ⇒ α = h−(((2/9)((h/9)−k))/(1+(1/(81)))) ⇒ 𝛂=h−(9/(41))((h/9)−k) and 𝛃 = k+((81)/(41))((h/9)−k) eq. of line through BC is y+h = ((β+h)/(α+k))(x+k) As this passes through P (a,b) b+h = ((β+h)/(α+k))(a+k) replacing α, β in terms of h,k and changing h,k to x,y we get the desired locus of A(third vertex) b+h=((k+((81)/(41))((h/9)−k)+h)/(h−(9/(41))((h/9)−k)+k))(a+k) ⇒ (b+x)[x+y−(9/(41))((x/9)−y)] = (a+y)[x+y+((81)/(41))((x/9)−y)] locus found is 40(x^2 +y^2 )−41(b−a)(x+y) −9(ax−by)=0 .](https://www.tinkutara.com/question/Q43015.png)
$${let}\:{A}\left({h},{k}\right) \\ $$$$\Rightarrow\:\:{B}\left(−{k},\:−{h}\right) \\ $$$${let}\:{C}\left(\alpha,\:\beta\right) \\ $$$${reflection}\:{of}\:{C}\:{in}\:{y}={mx}+{c}\:\:\:{is} \\ $$$$\alpha={h}−\frac{\mathrm{2}{m}\left({c}+{mh}−{k}\right)}{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\beta\:=\:{k}+\frac{\mathrm{2}\left({c}+{mh}−{k}\right)}{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${here}\:{we}\:{have}\:\:\boldsymbol{{y}}=\:\frac{\boldsymbol{{x}}}{\mathrm{9}} \\ $$$$\Rightarrow\:\:{m}=\frac{\mathrm{1}}{\mathrm{9}}\:,\:{c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\alpha\:=\:{h}−\frac{\frac{\mathrm{2}}{\mathrm{9}}\left(\frac{{h}}{\mathrm{9}}−{k}\right)}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{81}}} \\ $$$$\Rightarrow\:\:\boldsymbol{\alpha}=\boldsymbol{{h}}−\frac{\mathrm{9}}{\mathrm{41}}\left(\frac{\boldsymbol{{h}}}{\mathrm{9}}−\boldsymbol{{k}}\right) \\ $$$${and}\:\:\:\boldsymbol{\beta}\:=\:\boldsymbol{{k}}+\frac{\mathrm{81}}{\mathrm{41}}\left(\frac{\boldsymbol{{h}}}{\mathrm{9}}−\boldsymbol{{k}}\right) \\ $$$${eq}.\:{of}\:{line}\:{through}\:{BC}\:{is} \\ $$$${y}+{h}\:=\:\frac{\beta+{h}}{\alpha+{k}}\left({x}+{k}\right) \\ $$$${As}\:{this}\:{passes}\:{through}\:{P}\:\left({a},{b}\right) \\ $$$${b}+{h}\:=\:\frac{\beta+{h}}{\alpha+{k}}\left({a}+{k}\right) \\ $$$${replacing}\:\alpha,\:\beta\:{in}\:{terms}\:{of}\:{h},{k} \\ $$$${and}\:{changing}\:{h},{k}\:{to}\:{x},{y}\:{we}\:{get} \\ $$$${the}\:{desired}\:{locus}\:{of}\:{A}\left({third}\:{vertex}\right) \\ $$$$\boldsymbol{{b}}+\boldsymbol{{h}}=\frac{\boldsymbol{{k}}+\frac{\mathrm{81}}{\mathrm{41}}\left(\frac{\boldsymbol{{h}}}{\mathrm{9}}−\boldsymbol{{k}}\right)+\boldsymbol{{h}}}{\boldsymbol{{h}}−\frac{\mathrm{9}}{\mathrm{41}}\left(\frac{\boldsymbol{{h}}}{\mathrm{9}}−\boldsymbol{{k}}\right)+\boldsymbol{{k}}}\left(\boldsymbol{{a}}+\boldsymbol{{k}}\right) \\ $$$$\Rightarrow\:\left({b}+{x}\right)\left[{x}+{y}−\frac{\mathrm{9}}{\mathrm{41}}\left(\frac{{x}}{\mathrm{9}}−{y}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({a}+{y}\right)\left[{x}+{y}+\frac{\mathrm{81}}{\mathrm{41}}\left(\frac{{x}}{\mathrm{9}}−{y}\right)\right] \\ $$$${locus}\:\:{found}\:{is} \\ $$$$\:\:\:\mathrm{40}\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)−\mathrm{41}\left(\boldsymbol{{b}}−\boldsymbol{{a}}\right)\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{9}\left(\boldsymbol{{ax}}−\boldsymbol{{by}}\right)=\mathrm{0}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
$${dear}\:{ajfour}\:{sir}\:{which}\:{app}\:{helps}\:{to}\:{draw}\:…{for} \\ $$$${example}\:{this}\:{problem}… \\ $$
Commented by ajfour last updated on 06/Sep/18
$${lekh}\:{diagram}. \\ $$$${i}\:{have}\:{understood}\:{how}\:{to}\:{use}\:{it} \\ $$$${any}\:{confusion},\:{u}\:{can}\:{ask}\:{me}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
$${ok}\:{thank}\:{you}…{i}\:{have}\:{latent}\:{wish}\:{to}\:{see}\:{ourselves} \\ $$$${we}\:{are}\:{virtually}\:{connected}\:{but}\:{never}\:{see}\:{each}\:{other} \\ $$$${so}\:{if}\:{admin}\:{of}\:{this}\:{app}\:{give}\:{permission}\:{to}\:{upload} \\ $$$${our}\:{picture}\:{atleast}\:{onece}…{i} \\ $$
Commented by MJS last updated on 06/Sep/18
$$\mathrm{we}\:\mathrm{could}\:\mathrm{upload}\:\mathrm{a}\:\mathrm{self}\:\mathrm{portrait}\:\mathrm{including}\:\mathrm{a} \\ $$$$\mathrm{math}\:\mathrm{example}… \\ $$
Commented by mondodotto@gmail.com last updated on 06/Sep/18
$$\mathrm{thanx}\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
Commented by behi83417@gmail.com last updated on 06/Sep/18
$${wonderful}\:\:{idea}! \\ $$$${waiting}\:{for}\:{sir}:\:{MrW}\mathrm{3},{ajfour}, \\ $$$${sir}\:{MJS},{prop}.{Abdo}\:,….. \\ $$
Commented by MJS last updated on 06/Sep/18
Commented by MJS last updated on 06/Sep/18
$$\mathrm{the}\:\mathrm{man}\:\mathrm{is}\:\mathrm{1}.\mathrm{95m}\:\mathrm{tall},\:\mathrm{his}\:\mathrm{beard}\:\mathrm{is}\:\mathrm{half}\:\mathrm{as}\:\mathrm{long} \\ $$$$\mathrm{as}\:\mathrm{Santa}\:\mathrm{Claus}'\:.\:\mathrm{how}\:\mathrm{many}\:\mathrm{thorns}\:\mathrm{has}\:\mathrm{his} \\ $$$$\mathrm{cactus}\:\mathrm{if}\:\mathrm{the}\:\mathrm{temperature}\:\mathrm{is}\:\mathrm{35}°\mathrm{C}? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
$${excellent}…{sir}…{i}\:{have}\:{thought}\:{a}\:{virtual}\:{image}\: \\ $$$${of}\:{you}\:{sir}…{i}\:{shall}\:{post}…{what}\:{i}\:{imagined}\:{about} \\ $$$${you}\:{sir}… \\ $$$$ \\ $$
Commented by MJS last updated on 06/Sep/18
$$\mathrm{ha}!\:\mathrm{I}'\mathrm{d}\:\mathrm{like}\:\mathrm{to}\:\mathrm{see}\:\mathrm{it}! \\ $$
Commented by math khazana by abdo last updated on 07/Sep/18
$${we}\:{are}\:{waiting}\:{to}\:{know}\:{sir}\:{Tinkutara}\:,\:{sirAjfour}\:,{sir}\:{Mrw}\:,{sir} \\ $$$${Raul}\:,{sir}\:{Prakach}\:{jain}\:,{sir}\:{Smai}\mathrm{3}… \\ $$
Commented by malwaan last updated on 07/Sep/18
Commented by malwaan last updated on 07/Sep/18
$$\mathrm{that}\:\mathrm{is}\:\mathrm{me} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18
$${thank}\:{you}\:{sir}… \\ $$