Question Number 174185 by nadovic last updated on 26/Jul/22
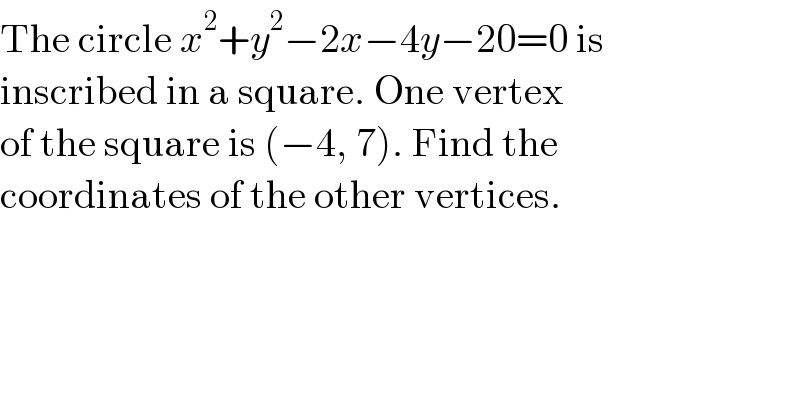
$$\mathrm{The}\:\mathrm{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}{y}−\mathrm{20}=\mathrm{0}\:\mathrm{is} \\ $$$$\mathrm{inscribed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{square}.\:\mathrm{One}\:\mathrm{vertex} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{is}\:\left(−\mathrm{4},\:\mathrm{7}\right).\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{coordinates}\:\mathrm{of}\:\mathrm{the}\:\mathrm{other}\:\mathrm{vertices}. \\ $$
Answered by Cesar1994 last updated on 26/Jul/22

$$ \\ $$$$ \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}{y}−\mathrm{20}=\mathrm{0}\:\Leftrightarrow\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{20}+\mathrm{1}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$${the}\:{circle}'{s}\:{center}\:{is}\:\left(\mathrm{1},\:\mathrm{2}\right) \\ $$$$\left(\frac{−\mathrm{3}−\mathrm{7}}{\mathrm{6}−\left(−\mathrm{4}\right)}\right)\left(\frac{−\mathrm{3}−\mathrm{7}}{−\mathrm{4}−\mathrm{6}}\right)=\frac{−\mathrm{10}}{\mathrm{10}}\left(\frac{−\mathrm{10}}{−\mathrm{10}}\right)=−\mathrm{1} \\ $$$${the}\:{diametrically}\:{oposite}\:{vertex}\:{to}\:{A}\left(−\mathrm{4},\mathrm{7}\right)\:{is}\:{B}\left(\mathrm{1}+\mathrm{5},\:\mathrm{2}−\mathrm{5}\right)={B}\left(\mathrm{6},−\mathrm{3}\right) \\ $$$${the}\:{others}\:{vertices}\:{are}\:{C}\left(\mathrm{1}+\mathrm{5},\:\mathrm{2}+\mathrm{5}\right)={C}\left(\mathrm{6},\mathrm{7}\right)\:{and}\:{D}\left(\mathrm{1}−\mathrm{5},\mathrm{2}−\mathrm{5}\right)={D}\left(−\mathrm{4},−\mathrm{3}\right) \\ $$$${evaluating}\:{each}\:{point}\:{in}\:\left(\mathrm{1}\right)\:{it}\:{is}\:{verified}\:{that}\:{they}\:{are}\:{on}\:{the}\:{circumference} \\ $$$${then}\:{prove}\:{that}\:{the}\:{diagonals}\:{AB}\:{and}\:{CD}\:{are}\:{perpendiculars}\:{one}\:{to}\:{the}\:{other} \\ $$$$\left(\frac{−\mathrm{3}−\mathrm{7}}{\mathrm{6}−\left(−\mathrm{4}\right)}\right)\left(\frac{−\mathrm{3}−\mathrm{7}}{−\mathrm{4}−\mathrm{6}}\right)=\frac{−\mathrm{10}}{\mathrm{10}}\left(\frac{−\mathrm{10}}{−\mathrm{10}}\right)=−\mathrm{1} \\ $$$$\therefore\:{the}\:{ABCD}\:{is}\:{rhombus} \\ $$$${then}\:{side}\:{AC}\:{is}\:{horizontal}\:{and}\:{side}\:{BC}\:{is}\:{vertical}\:{side},\:{so}\:{they}\:{are}\:{perpendicular} \\ $$$$\therefore\:{ABCD}\:{is}\:{a}\:{square}\:\blacksquare \\ $$
