Question Number 174094 by nadovic last updated on 24/Jul/22
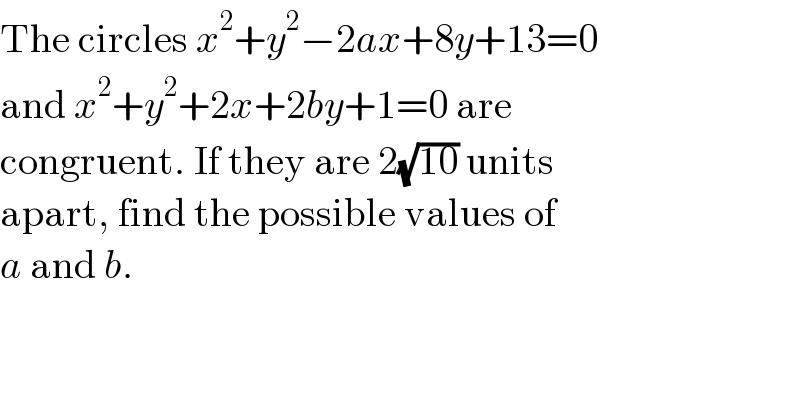
$$\mathrm{The}\:\mathrm{circles}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ax}+\mathrm{8}{y}+\mathrm{13}=\mathrm{0} \\ $$$$\mathrm{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}{by}+\mathrm{1}=\mathrm{0}\:\mathrm{are}\: \\ $$$$\mathrm{congruent}.\:\mathrm{If}\:\mathrm{they}\:\mathrm{are}\:\mathrm{2}\sqrt{\mathrm{10}}\:\mathrm{units}\: \\ $$$$\mathrm{apart},\:\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of} \\ $$$${a}\:\mathrm{and}\:{b}. \\ $$
Answered by a.lgnaoui last updated on 25/Jul/22
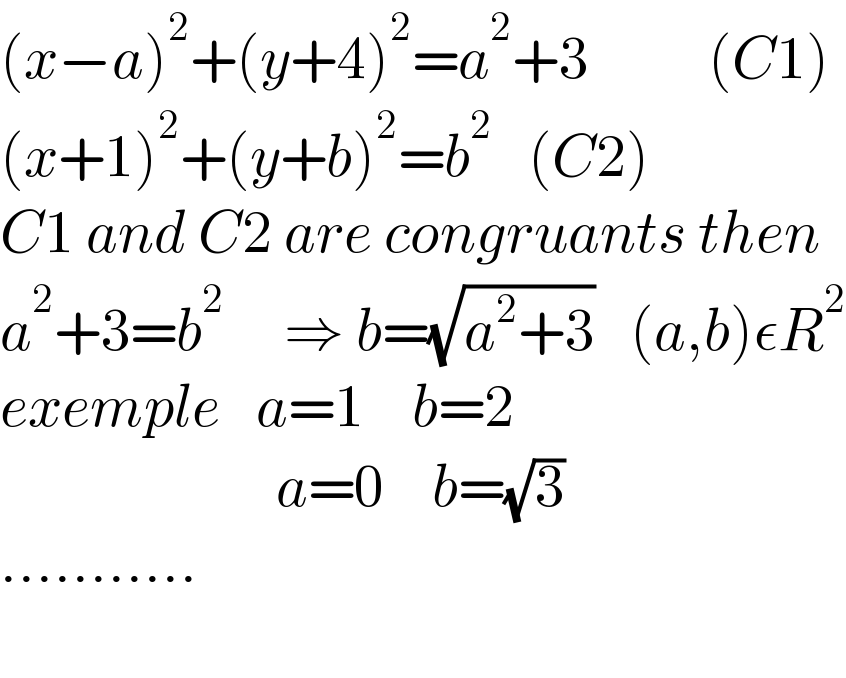
$$\left({x}−{a}\right)^{\mathrm{2}} +\left({y}+\mathrm{4}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{3}\:\:\:\:\:\:\:\:\:\:\left({C}\mathrm{1}\right) \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\left({y}+{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \:\:\:\left({C}\mathrm{2}\right) \\ $$$${C}\mathrm{1}\:{and}\:{C}\mathrm{2}\:{are}\:{congruants}\:{then} \\ $$$${a}^{\mathrm{2}} +\mathrm{3}={b}^{\mathrm{2}} \:\:\:\:\:\Rightarrow\:{b}=\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}\:\:\:\left({a},{b}\right)\epsilon{R}^{\mathrm{2}} \\ $$$${exemple}\:\:\:{a}=\mathrm{1}\:\:\:\:{b}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\mathrm{0}\:\:\:\:{b}=\sqrt{\mathrm{3}}\: \\ $$$$……….. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
