The-coefficient-of-x-4-in-2-4x-3x-2-2-i-s-

Question Number 54024 by sandip123 last updated on 28/Jan/19

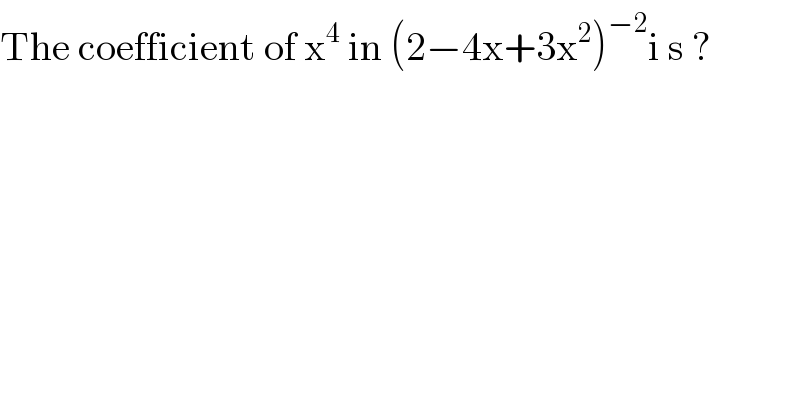
The coefficient of x^{4} in {(2 - 4 x + {3 x}^{2})}^{- 2} i s ?

Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19

{(2 - 4 x + 3 x^{2})}^{- 2}

= {2 - (4 x - 3 x^{2})}^{- 2}

= 2^{- 2} {1 - (\frac{4 x - 3 x^{2}}{2})}^{- 2}

n o w u s i n g f o r m u l a

{(1 - y)}^{- 2} = 1 + 2 y + 3 y^{2} + 4 y^{3} + \dots + (r + 1) x^{r} + \dots

= 2^{- 2} [1 + 2 (\frac{4 x - 3 x^{2}}{2}) + 3 {(\frac{4 x - 3 x^{2}}{2})}^{2} + 4 {(\frac{4 x - 3 x^{2}}{2})}^{3} + 5 {(\frac{4 x - 3 x^{2}}{2})}^{4} + \dots

= 2^{- 2} [1 + 4 x - 3 x^{2} + \frac{3}{4} (4 x^{2} - 24 x^{3} + 9 x^{4}) + \frac{4}{8} (64 x^{3} - 3 \times 16 x^{2} \times 3 x^{2} + 3 \times 4 x \times 9 x^{4} - 27 x^{6}) + \frac{5}{2^{4}} (4^{4} x^{4} + o t h e r s i g n o r e d)

i g n o r i n g r e d m a r k e d \dots

= 2^{- 2} [\frac{3}{4} \times 9 x^{4} + \frac{4}{8} \times - 9 \times 16 \times x^{4} + \frac{5}{2^{4}} \times 4^{4} x^{4}]

= x^{4} [\frac{3 \times 9}{4 \times 2^{2}} - \frac{4 \times 9 \times 16}{2^{2} \times 8} + \frac{5 \times 4^{4}}{2^{4} \times 2^{2}}]

= x^{4} [\frac{27}{16} - \frac{18}{1} + \frac{5 \times 2^{8}}{2^{6}}]

= x^{4} [\frac{27}{16} - \frac{18}{1} + \frac{5 \times 2^{2}}{1}]

= x^{4} [\frac{27}{26} + 2] s o c o e f f i c i e n t = \frac{79}{26}

p l s c h e c k s t e p s \dots

Commented by sandip123 last updated on 01/Feb/19

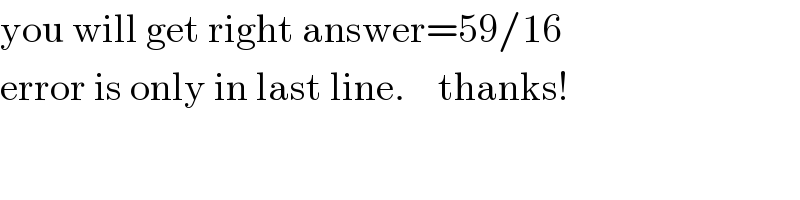
you will get right answer = 59 / 16

error is only in last line . thanks!