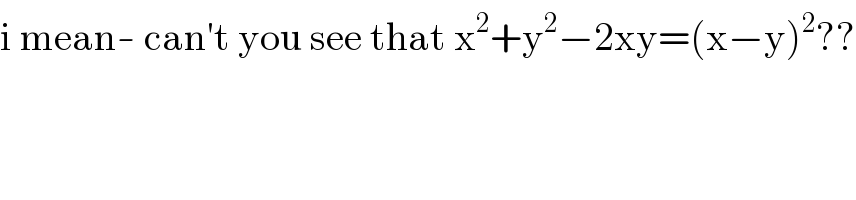The-Diophantine-equation-x-2-y-2-1-N-xy-1-has-infinitely-many-integer-solutions-if-N-equals-Any-help-please-

Question Number 110644 by Aina Samuel Temidayo last updated on 29/Aug/20

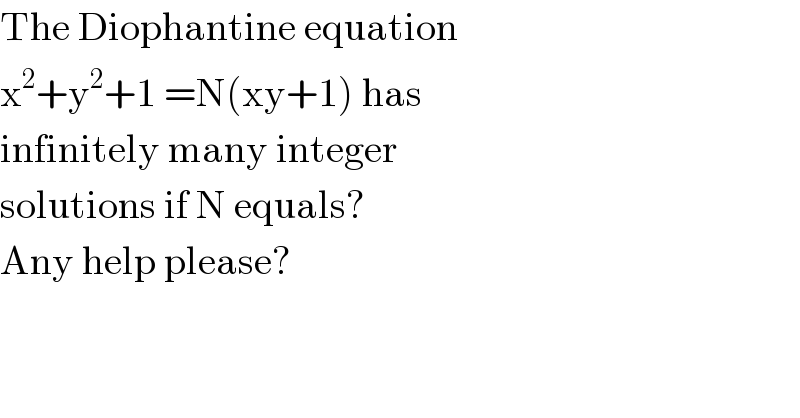
The Diophantine equation

x^{2} + y^{2} + 1 = N (xy + 1) has

infinitely many integer

solutions if N equals ?

Any help please ?

Commented by Aina Samuel Temidayo last updated on 30/Aug/20

No one has been able to solve this ?

Answered by floor(10²Eta[1]) last updated on 30/Aug/20

if N = 2

x^{2} + y^{2} + 1 = 2 xy + 2

{(x - y)}^{2} = 1 \Rightarrow x - y = \pm 1

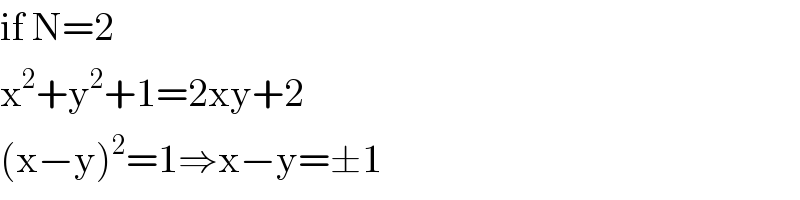
Commented by Aina Samuel Temidayo last updated on 30/Aug/20

Yes but how did you arrive at N = 2 ?

Commented by floor(10²Eta[1]) last updated on 30/Aug/20

i mean - {can}^{'} t you see that x^{2} + y^{2} - 2 xy = {(x - y)}^{2} ? ?