The-drawing-below-shows-two-equilateral-triangles-with-side-length-a-The-triangle-are-horizontally-shifted-by-a-2-Find-the-intersection-area-A-of-the-two-triangles-grey-area-

Question Number 174591 by Mastermind last updated on 05/Aug/22

The drawing below shows two

equilateral triangles with side length

a . The triangle are horizontally shifted

by \frac{a}{2} . Find the intersection area A of

the two triangles (grey area) .

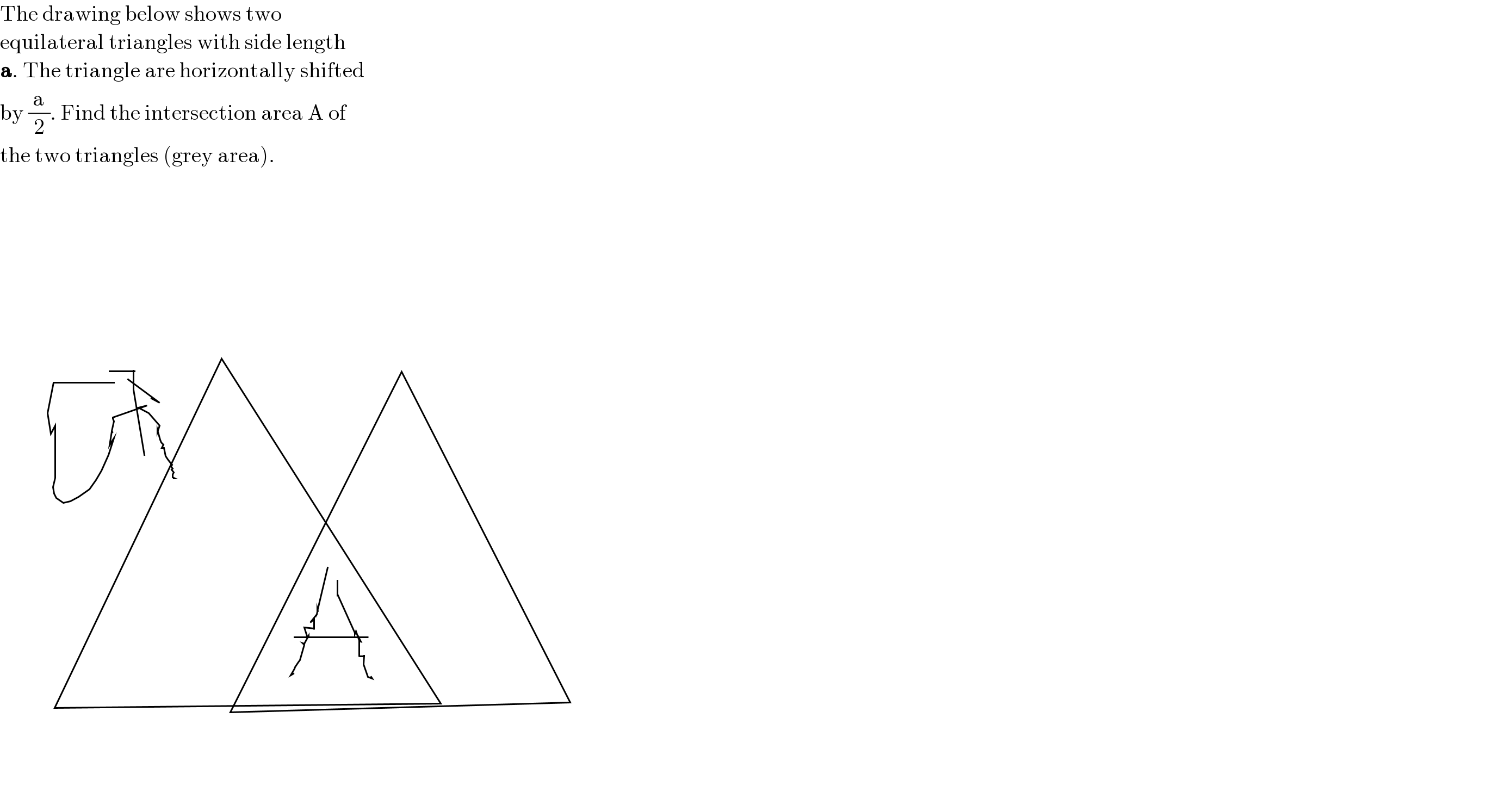
Answered by behi834171 last updated on 05/Aug/22

a s l o h a v e a n e q u i l a t e r a l t r i a n g l e

w i t h s i d e l e n g h t : \frac{a}{2}

s o, w a n t e d a r e a = \frac{{(\frac{a}{2})}^{2}}{4} \sqrt{3} = \frac{a^{2} \sqrt{3}}{16} .

Commented by Mastermind last updated on 05/Aug/22

I did not understand what {you}^{'} re trying

to say here, explain it well

Commented by Mastermind last updated on 05/Aug/22

Commented by behi834171 last updated on 05/Aug/22

4 A = \frac{a^{2} \sqrt{3}}{4} \Rightarrow A = \frac{a^{2} \sqrt{3}}{16} .

4 o f s u c h s h a d e d a r e a s = w h o l e o f a

e q u i l a t e r a l t r i a n g l e w i t h s i d e : a

t h a t {i t}^{'} s a r e a = \frac{a^{2} \sqrt{3}}{4} .

i g o t w h a t y o u m e a n t s i r .

i t i s t o o e a s y t o s a y m o r e \dots .

Commented by Mastermind last updated on 05/Aug/22

Tank you so much man