Question Number 148219 by iloveisrael last updated on 26/Jul/21
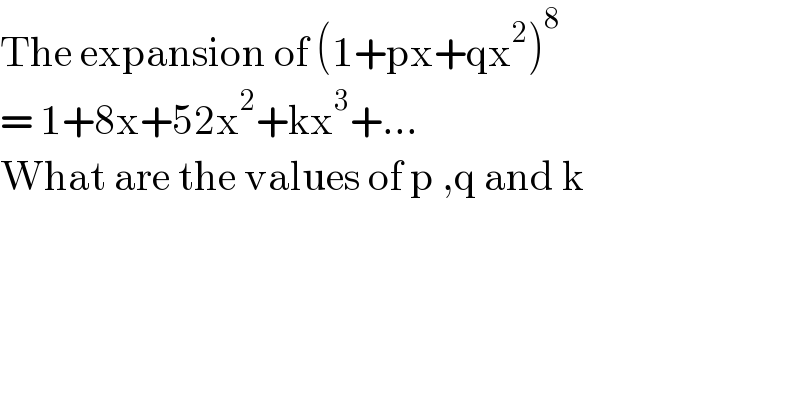
$$\mathrm{The}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{px}+\mathrm{qx}^{\mathrm{2}} \right)^{\mathrm{8}} \: \\ $$$$=\:\mathrm{1}+\mathrm{8x}+\mathrm{52x}^{\mathrm{2}} +\mathrm{kx}^{\mathrm{3}} +… \\ $$$$\mathrm{What}\:\mathrm{are}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{p}\:,\mathrm{q}\:\mathrm{and}\:\mathrm{k} \\ $$
Answered by liberty last updated on 26/Jul/21

$${by}\:{Trinomial}\:{theorem}\: \\ $$$$\left(\mathrm{1}+{px}+{qx}^{\mathrm{2}} \right)^{\mathrm{8}} =\underset{\alpha+\beta+\gamma=\mathrm{8}} {\sum}\mathrm{1}^{\alpha} \left({px}\right)^{\beta} \left({qx}^{\mathrm{2}} \right)^{\gamma} \\ $$$$\left({i}\right)\:{x}−{term}\:=\:\frac{\mathrm{8}!}{\mathrm{7}!\mathrm{1}!\mathrm{0}!}\left({px}\right)^{\mathrm{1}} =\mathrm{8}{px} \\ $$$$\left({ii}\right){x}^{\mathrm{2}} −{term}=\frac{\mathrm{8}!}{\mathrm{6}!\mathrm{2}!\mathrm{0}!}\left({px}\right)^{\mathrm{2}} +\frac{\mathrm{8}!}{\mathrm{7}!\mathrm{0}!\mathrm{1}!}\left({qx}^{\mathrm{2}} \right)^{\mathrm{1}} =\left(\mathrm{28}{p}^{\mathrm{2}} +\mathrm{8}{q}\right){x}^{\mathrm{2}} \\ $$$$\left({iii}\right){x}^{\mathrm{3}} −{term}=\frac{\mathrm{8}!}{\mathrm{5}!\mathrm{3}!\mathrm{0}!}\left({px}\right)^{\mathrm{3}} +\frac{\mathrm{8}!}{\mathrm{6}!\mathrm{1}!\mathrm{1}!}\left({px}\right)^{\mathrm{1}} \left({qx}^{\mathrm{2}} \right)^{\mathrm{1}} \\ $$$$=\:\left(\mathrm{56}{p}^{\mathrm{3}} +\mathrm{56}{pq}\right){x}^{\mathrm{3}} \\ $$$${comparing}\:{coefficients} \\ $$$$\begin{cases}{\mathrm{8}{p}=\mathrm{8}\Rightarrow{p}=\mathrm{1}}\\{\mathrm{28}{p}^{\mathrm{2}} +\mathrm{8}{q}=\mathrm{52}\Rightarrow{q}=\mathrm{3}}\\{\mathrm{56}{p}^{\mathrm{3}} +\mathrm{56}{pq}={k}\Rightarrow{k}=\mathrm{224}}\end{cases} \\ $$
