Question Number 18472 by Tinkutara last updated on 22/Jul/17
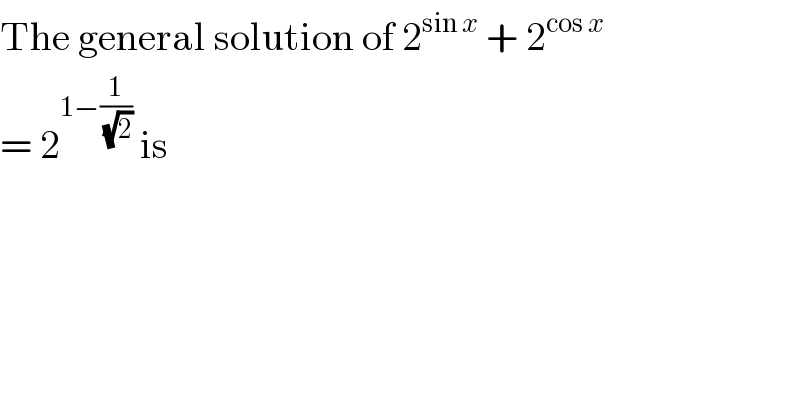
$$\mathrm{The}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{2}^{\mathrm{sin}\:{x}} \:+\:\mathrm{2}^{\mathrm{cos}\:{x}} \\ $$$$=\:\mathrm{2}^{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \:\mathrm{is} \\ $$
Answered by sushmitak last updated on 22/Jul/17
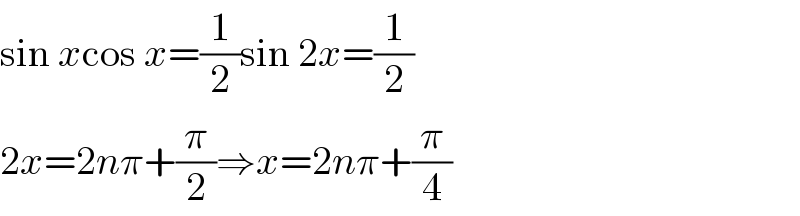
$$\mathrm{sin}\:{x}\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{2}}\Rightarrow{x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{4}} \\ $$
Commented by sushmitak last updated on 23/Jul/17
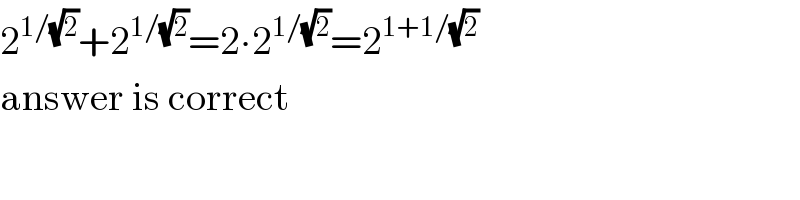
$$\mathrm{2}^{\mathrm{1}/\sqrt{\mathrm{2}}} +\mathrm{2}^{\mathrm{1}/\sqrt{\mathrm{2}}} =\mathrm{2}\centerdot\mathrm{2}^{\mathrm{1}/\sqrt{\mathrm{2}}} =\mathrm{2}^{\mathrm{1}+\mathrm{1}/\sqrt{\mathrm{2}}} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$
Commented by Tinkutara last updated on 23/Jul/17

$$\mathrm{But}\:\mathrm{it}\:\mathrm{is}\:\mathrm{2}^{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} . \\ $$
