Question Number 53426 by Necxx last updated on 21/Jan/19
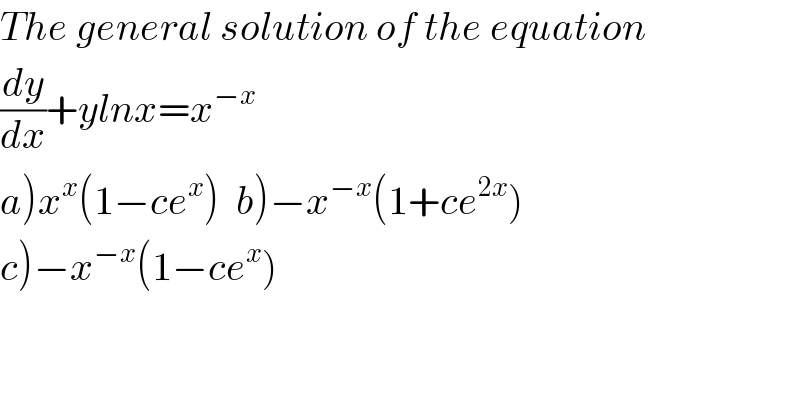
$${The}\:{general}\:{solution}\:{of}\:{the}\:{equation} \\ $$$$\frac{{dy}}{{dx}}+{ylnx}={x}^{−{x}} \\ $$$$\left.{a}\left.\right){x}^{{x}} \left(\mathrm{1}−{ce}^{{x}} \right)\:\:{b}\right)−{x}^{−{x}} \left(\mathrm{1}+{ce}^{\mathrm{2}{x}} \right) \\ $$$$\left.{c}\right)−{x}^{−{x}} \left(\mathrm{1}−{ce}^{{x}} \right) \\ $$
Commented by maxmathsup by imad last updated on 26/May/19
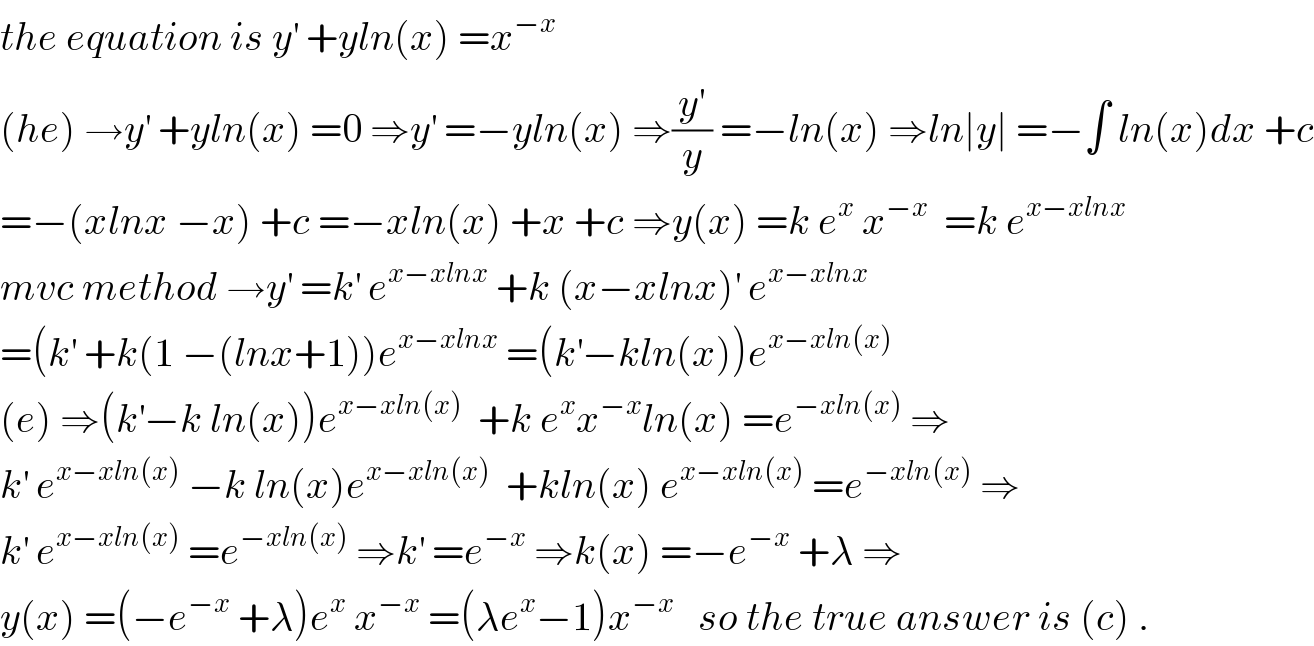
$${the}\:{equation}\:{is}\:{y}^{'} \:+{yln}\left({x}\right)\:={x}^{−{x}} \\ $$$$\left({he}\right)\:\rightarrow{y}^{'} \:+{yln}\left({x}\right)\:=\mathrm{0}\:\Rightarrow{y}^{'} \:=−{yln}\left({x}\right)\:\Rightarrow\frac{{y}^{'} }{{y}}\:=−{ln}\left({x}\right)\:\Rightarrow{ln}\mid{y}\mid\:=−\int\:{ln}\left({x}\right){dx}\:+{c} \\ $$$$=−\left({xlnx}\:−{x}\right)\:+{c}\:=−{xln}\left({x}\right)\:+{x}\:+{c}\:\Rightarrow{y}\left({x}\right)\:={k}\:{e}^{{x}} \:{x}^{−{x}} \:\:={k}\:{e}^{{x}−{xlnx}} \\ $$$${mvc}\:{method}\:\rightarrow{y}^{'} \:={k}^{'} \:{e}^{{x}−{xlnx}} \:+{k}\:\left({x}−{xlnx}\right)^{'} \:{e}^{{x}−{xlnx}} \\ $$$$=\left({k}^{'} \:+{k}\left(\mathrm{1}\:−\left({lnx}+\mathrm{1}\right)\right){e}^{{x}−{xlnx}} \:=\left({k}^{'} −{kln}\left({x}\right)\right){e}^{{x}−{xln}\left({x}\right)} \right. \\ $$$$\left({e}\right)\:\Rightarrow\left({k}^{'} −{k}\:{ln}\left({x}\right)\right){e}^{{x}−{xln}\left({x}\right)} \:\:+{k}\:{e}^{{x}} {x}^{−{x}} {ln}\left({x}\right)\:={e}^{−{xln}\left({x}\right)} \:\Rightarrow \\ $$$${k}^{'} \:{e}^{{x}−{xln}\left({x}\right)} \:−{k}\:{ln}\left({x}\right){e}^{{x}−{xln}\left({x}\right)} \:\:+{kln}\left({x}\right)\:{e}^{{x}−{xln}\left({x}\right)} \:={e}^{−{xln}\left({x}\right)} \:\Rightarrow \\ $$$${k}^{'} \:{e}^{{x}−{xln}\left({x}\right)} \:={e}^{−{xln}\left({x}\right)} \:\Rightarrow{k}^{'} \:={e}^{−{x}} \:\Rightarrow{k}\left({x}\right)\:=−{e}^{−{x}} \:+\lambda\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\left(−{e}^{−{x}} \:+\lambda\right){e}^{{x}} \:{x}^{−{x}} \:=\left(\lambda{e}^{{x}} −\mathrm{1}\right){x}^{−{x}} \:\:\:{so}\:{the}\:{true}\:{answer}\:{is}\:\left({c}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19
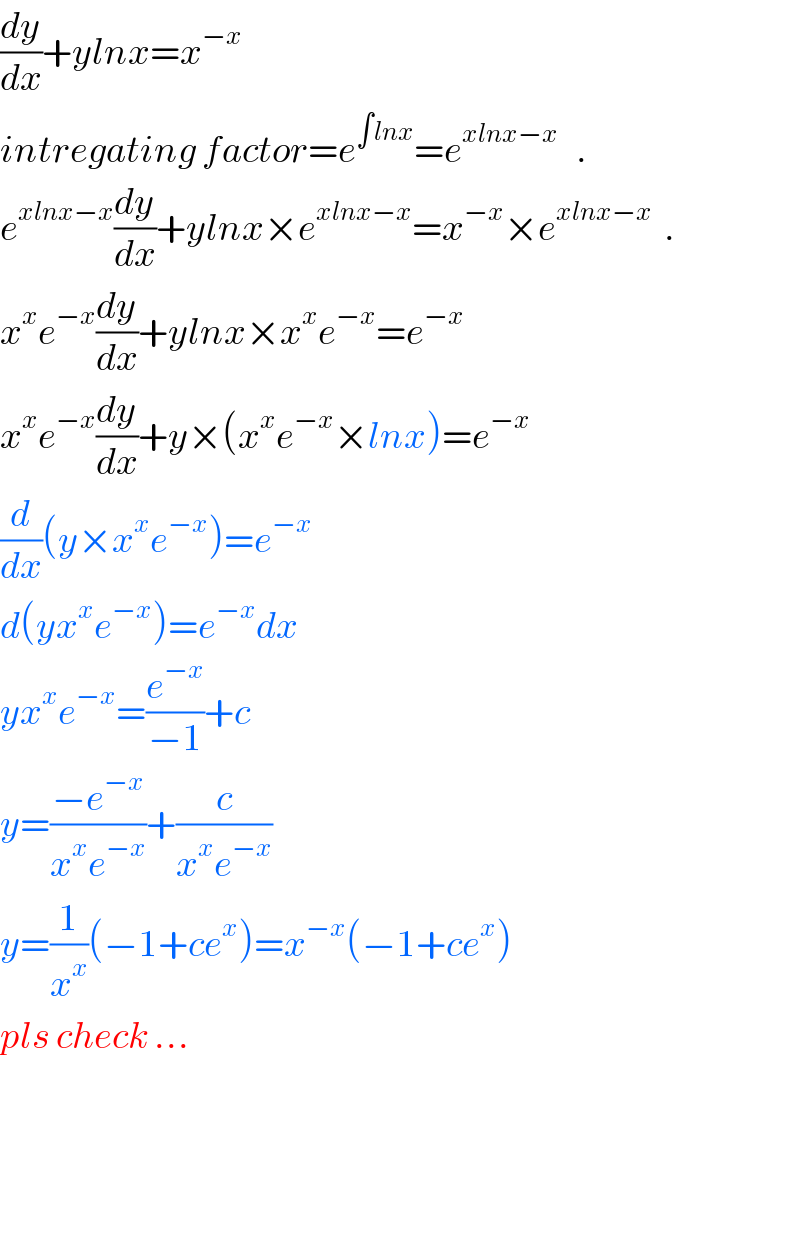
$$\frac{{dy}}{{dx}}+{ylnx}={x}^{−{x}} \\ $$$${intregating}\:{factor}={e}^{\int{lnx}} ={e}^{{xlnx}−{x}} \:\:\:. \\ $$$${e}^{{xlnx}−{x}} \frac{{dy}}{{dx}}+{ylnx}×{e}^{{xlnx}−{x}} ={x}^{−{x}} ×{e}^{{xlnx}−{x}} \:\:. \\ $$$${x}^{{x}} {e}^{−{x}} \frac{{dy}}{{dx}}+{ylnx}×{x}^{{x}} {e}^{−{x}} ={e}^{−{x}} \\ $$$${x}^{{x}} {e}^{−{x}} \frac{{dy}}{{dx}}+{y}×\left({x}^{{x}} {e}^{−{x}} ×{lnx}\right)={e}^{−{x}} \\ $$$$\frac{{d}}{{dx}}\left({y}×{x}^{{x}} {e}^{−{x}} \right)={e}^{−{x}} \\ $$$${d}\left({yx}^{{x}} {e}^{−{x}} \right)={e}^{−{x}} {dx} \\ $$$${yx}^{{x}} {e}^{−{x}} =\frac{{e}^{−{x}} }{−\mathrm{1}}+{c} \\ $$$${y}=\frac{−{e}^{−{x}} }{{x}^{{x}} {e}^{−{x}} }+\frac{{c}}{{x}^{{x}} {e}^{−{x}} } \\ $$$${y}=\frac{\mathrm{1}}{{x}^{{x}} }\left(−\mathrm{1}+{ce}^{{x}} \right)={x}^{−{x}} \left(−\mathrm{1}+{ce}^{{x}} \right) \\ $$$${pls}\:{check}\:… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Necxx last updated on 22/Jan/19
$${oh}…..{thanks}\:{so}\:{much} \\ $$
