The-imaginary-part-of-1-2-1-2-i-10-is-

Question Number 58402 by rahul 19 last updated on 22/Apr/19

$${The}\:{imaginary}\:{part}\:{of}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}\right)^{\mathrm{10}} {is}\:? \\ $$

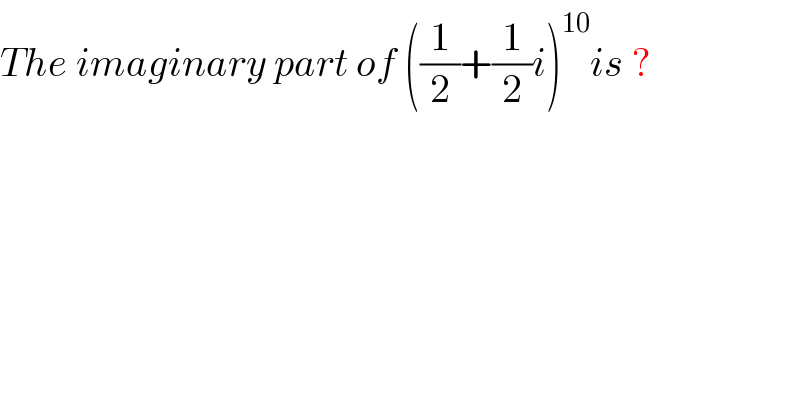
Commented by maxmathsup by imad last updated on 23/Apr/19

let Z =((1/2)+(1/2)i)^(10) ⇒Z =(1/2^(10) ) (1+i)^(10) =(1/2^(10) ) ((√2))^(10) (e^((iπ)/4) )^(10) =(1/2^5 ) e^(i((5π)/2)) =(1/2^5 ) e^((iπ)/2) =(1/2^5 ) {cos((π/2))+isin((π/2))} =(i/2^5 ) ⇒Im(Z) =(1/2^5 )

$${let}\:{Z}\:=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}\right)^{\mathrm{10}} \:\Rightarrow{Z}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\:\left(\mathrm{1}+{i}\right)^{\mathrm{10}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{10}} \:\left({e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{\mathrm{10}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:{e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:{e}^{\frac{{i}\pi}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:\left\{{cos}\left(\frac{\pi}{\mathrm{2}}\right)+{isin}\left(\frac{\pi}{\mathrm{2}}\right)\right\}\:\:=\frac{{i}}{\mathrm{2}^{\mathrm{5}} }\:\Rightarrow{Im}\left({Z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} } \\ $$

Commented by rahul 19 last updated on 23/Apr/19

$${thanks}\:{sir}! \\ $$

Answered by tanmay last updated on 23/Apr/19

(1/2^(10) )((1+i)^(10) =(1/2^(10) )[(√2) ((1/( (√2) ))+(1/( (√2)))i)]^(10) (1/2^(10) )×2^5 [cos(π/4)+isin(π/4)]^(10) =(1/2^5 )[cos(((5π)/2))+isin(((5π)/2))] =(1/2^5 )[0+i] =i ×(1/2^5 ) =real part=0 imaginary=1×(1/2^5 )

$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\left(\left(\mathrm{1}+{i}\right)^{\mathrm{10}} \right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\left[\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)\right]^{\mathrm{10}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }×\mathrm{2}^{\mathrm{5}} \left[{cos}\frac{\pi}{\mathrm{4}}+{isin}\frac{\pi}{\mathrm{4}}\right]^{\mathrm{10}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\left[{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{2}}\right)+{isin}\left(\frac{\mathrm{5}\pi}{\mathrm{2}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\left[\mathrm{0}+{i}\right] \\ $$$$={i}\:×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$={real}\:{part}=\mathrm{0} \\ $$$${imaginary}=\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$ \\ $$

Commented by rahul 19 last updated on 22/Apr/19

Ans→(1/2^5 ) [∵(1/2^(10) ) will be taken as common in 1st step]. thanks sir.... good night & sweet dreams:)

$${Ans}\rightarrow\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:\left[\because\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\:{will}\:{be}\:{taken}\:{as}\:{common}\right. \\ $$$$\left.{in}\:\mathrm{1}{st}\:{step}\right]. \\ $$$${thanks}\:{sir}…. \\ $$$$\left.\:{good}\:{night}\:\&\:\:{sweet}\:{dreams}:\right) \\ $$

Commented by tanmay last updated on 23/Apr/19

thank you rahul...shutter of window of mind (eyes) got fatigued ...so ....

$${thank}\:{you}\:{rahul}…{shutter}\:{of}\:{window}\:{of}\:{mind} \\ $$$$\left({eyes}\right)\:{got}\:{fatigued}\:…{so}\:…. \\ $$

Answered by MJS last updated on 23/Apr/19

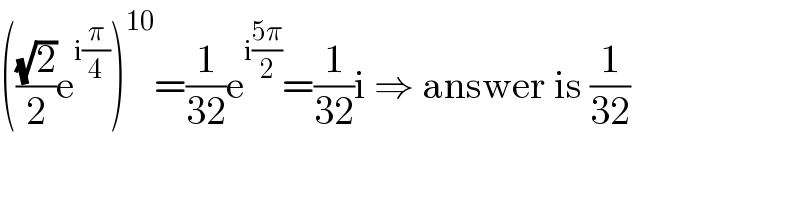
(((√2)/2)e^(i(π/4)) )^(10) =(1/(32))e^(i((5π)/2)) =(1/(32))i ⇒ answer is (1/(32))

$$\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{32}}\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{32}}\mathrm{i}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{32}} \\ $$

Commented by rahul 19 last updated on 23/Apr/19

$${thanks}\:{sir}! \\ $$

Facebook Tweet Pin

The-imaginary-part-of-1-2-1-2-i-10-is-

Leave a Reply Cancel reply