Menu Close

The-kinetic-energy-of-a-body-increases-by-100-Find-the-increase-in-its-momentum-please-solve-with-explanations-where-necessary-Thanks-

Tinku Tara 0 Comments
Pin




Question Number 21490 by NECx last updated on 24/Sep/17
The kinetic energy of a body increases by 100%.Find the % increase in its momentum. please solve with explanations where necessary. Thanks.
$$\mathrm{The}\:\mathrm{kinetic}\:\mathrm{energy}\:\mathrm{of}\:\mathrm{a}\:\mathrm{body} \\ $$$$\mathrm{increases}\:\mathrm{by}\:\mathrm{100\%}.\mathrm{Find}\:\mathrm{the}\:\% \\ $$$$\mathrm{increase}\:\mathrm{in}\:\mathrm{its}\:\mathrm{momentum}. \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{solve}\:\mathrm{with}\:\mathrm{explanations} \\ $$$$\mathrm{where}\:\mathrm{necessary}.\:\mathrm{Thanks}. \\ $$
Answered by ajfour last updated on 25/Sep/17
(p_1 ^2 /(2m)) =K_1 (p_2 ^2 /(2m))=K_2 ((K_2 −K_1 )/K_1 )×100=100 ⇒ ((p_2 ^2 −p_1 ^2 )/p_1 ^2 )×100=100 ((p_2 /p_1 ))^2 −1=1 ⇒ ((p_2 /p_1 ))^2 =2 % change in momentum is ((p_2 −p_1 )/p_1 )×100 = ((√2)−1)×100 = 41.4% . unless the change is differential change you cannot differentiate to get the correct answer.
$$\frac{{p}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}{m}}\:={K}_{\mathrm{1}} \\ $$$$\frac{{p}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}{m}}={K}_{\mathrm{2}} \\ $$$$\frac{{K}_{\mathrm{2}} −{K}_{\mathrm{1}} }{{K}_{\mathrm{1}} }×\mathrm{100}=\mathrm{100} \\ $$$$\Rightarrow\:\:\frac{{p}_{\mathrm{2}} ^{\mathrm{2}} −{p}_{\mathrm{1}} ^{\mathrm{2}} }{{p}_{\mathrm{1}} ^{\mathrm{2}} }×\mathrm{100}=\mathrm{100} \\ $$$$\left(\frac{{p}_{\mathrm{2}} }{{p}_{\mathrm{1}} }\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{1}\:\:\:\:\Rightarrow\:\:\:\:\left(\frac{{p}_{\mathrm{2}} }{{p}_{\mathrm{1}} }\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\%\:{change}\:{in}\:{momentum}\:{is} \\ $$$$\frac{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }{{p}_{\mathrm{1}} }×\mathrm{100}\:=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)×\mathrm{100} \\ $$$$=\:\mathrm{41}.\mathrm{4\%}\:. \\ $$$${unless}\:{the}\:{change}\:{is}\:{differential} \\ $$$${change}\:{you}\:{cannot}\:{differentiate}\: \\ $$$${to}\:{get}\:{the}\:{correct}\:{answer}. \\ $$
Commented by NECx last updated on 25/Sep/17
Mr Ajfour please this solution isnt explanatory to me. help simplify.
$$\mathrm{Mr}\:\mathrm{Ajfour}\:\mathrm{please}\:\mathrm{this}\:\mathrm{solution}\: \\ $$$$\mathrm{isnt}\:\mathrm{explanatory}\:\mathrm{to}\:\mathrm{me}.\:\mathrm{help} \\ $$$$\mathrm{simplify}. \\ $$
Commented by NECx last updated on 25/Sep/17
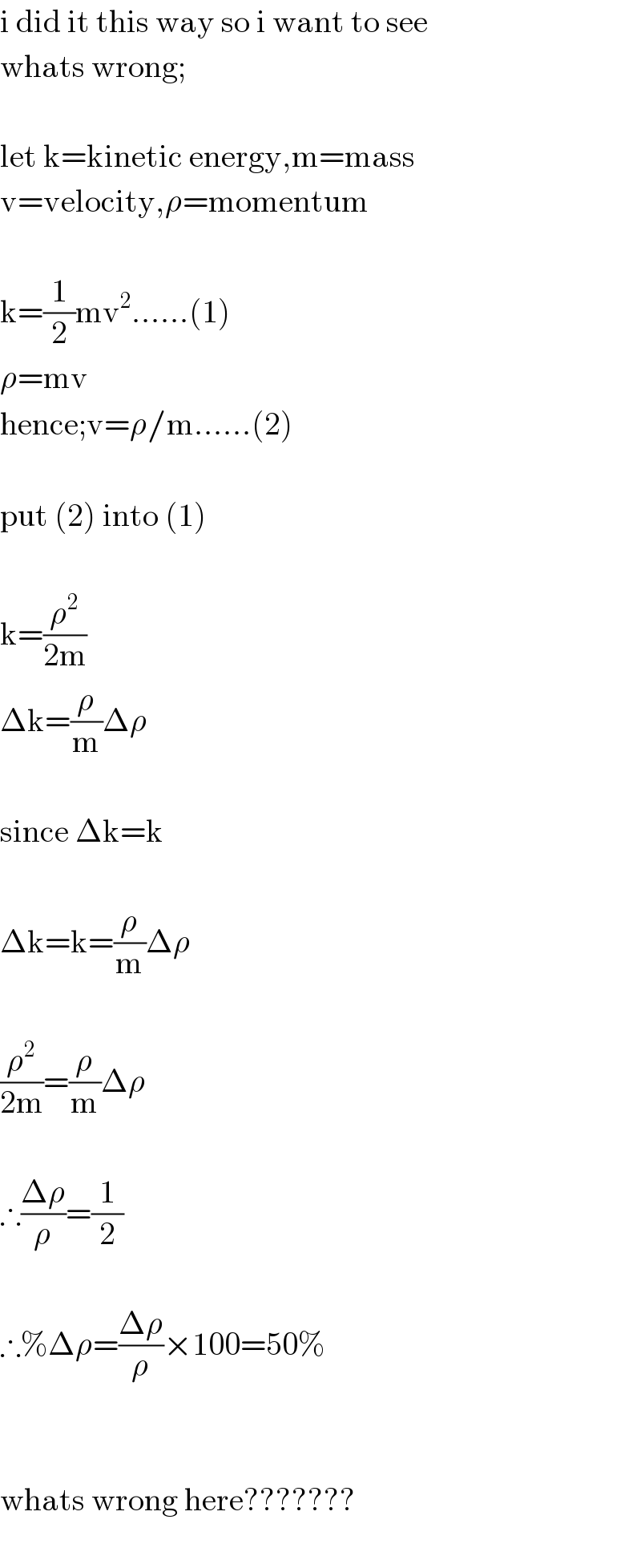
i did it this way so i want to see whats wrong; let k=kinetic energy,m=mass v=velocity,ρ=momentum k=(1/2)mv^2 ......(1) ρ=mv hence;v=ρ/m......(2) put (2) into (1) k=(ρ^2 /(2m)) Δk=(ρ/m)Δρ since Δk=k Δk=k=(ρ/m)Δρ (ρ^2 /(2m))=(ρ/m)Δρ ∴((Δρ)/ρ)=(1/2) ∴%Δρ=((Δρ)/ρ)×100=50% whats wrong here???????
$$\mathrm{i}\:\mathrm{did}\:\mathrm{it}\:\mathrm{this}\:\mathrm{way}\:\mathrm{so}\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{whats}\:\mathrm{wrong}; \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{k}=\mathrm{kinetic}\:\mathrm{energy},\mathrm{m}=\mathrm{mass} \\ $$$$\mathrm{v}=\mathrm{velocity},\rho=\mathrm{momentum} \\ $$$$ \\ $$$$\mathrm{k}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{mv}^{\mathrm{2}} ……\left(\mathrm{1}\right) \\ $$$$\rho=\mathrm{mv} \\ $$$$\mathrm{hence};\mathrm{v}=\rho/\mathrm{m}……\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{put}\:\left(\mathrm{2}\right)\:\mathrm{into}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{k}=\frac{\rho^{\mathrm{2}} }{\mathrm{2m}} \\ $$$$\Delta\mathrm{k}=\frac{\rho}{\mathrm{m}}\Delta\rho \\ $$$$ \\ $$$$\mathrm{since}\:\Delta\mathrm{k}=\mathrm{k} \\ $$$$ \\ $$$$\Delta\mathrm{k}=\mathrm{k}=\frac{\rho}{\mathrm{m}}\Delta\rho \\ $$$$ \\ $$$$\frac{\rho^{\mathrm{2}} }{\mathrm{2m}}=\frac{\rho}{\mathrm{m}}\Delta\rho \\ $$$$ \\ $$$$\therefore\frac{\Delta\rho}{\rho}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\therefore\%\Delta\rho=\frac{\Delta\rho}{\rho}×\mathrm{100}=\mathrm{50\%} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{whats}\:\mathrm{wrong}\:\mathrm{here}??????? \\ $$$$ \\ $$
Commented by Joel577 last updated on 25/Sep/17
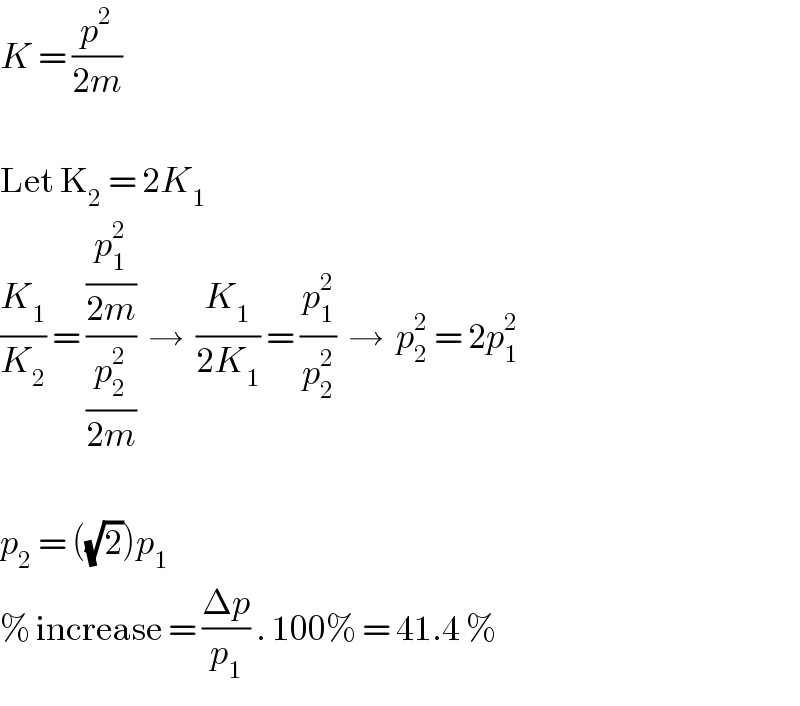
K = (p^2 /(2m)) Let K_2 = 2K_1 (K_1 /K_2 ) = ((p_1 ^2 /(2m))/(p_2 ^2 /(2m))) → (K_1 /(2K_1 )) = (p_1 ^2 /p_2 ^2 ) → p_2 ^2 = 2p_1 ^2 p_2 = ((√2))p_1 % increase = ((Δp)/p_1 ) . 100% = 41.4 %
$${K}\:=\:\frac{{p}^{\mathrm{2}} }{\mathrm{2}{m}} \\ $$$$ \\ $$$$\mathrm{Let}\:\mathrm{K}_{\mathrm{2}} \:=\:\mathrm{2}{K}_{\mathrm{1}} \\ $$$$\frac{{K}_{\mathrm{1}} }{{K}_{\mathrm{2}} }\:=\:\frac{\frac{{p}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}{m}}}{\frac{{p}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}{m}}}\:\:\rightarrow\:\:\frac{{K}_{\mathrm{1}} }{\mathrm{2}{K}_{\mathrm{1}} }\:=\:\frac{{p}_{\mathrm{1}} ^{\mathrm{2}} }{{p}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\rightarrow\:\:{p}_{\mathrm{2}} ^{\mathrm{2}} \:=\:\mathrm{2}{p}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$ \\ $$$${p}_{\mathrm{2}} \:=\:\left(\sqrt{\mathrm{2}}\right){p}_{\mathrm{1}} \\ $$$$\%\:\mathrm{increase}\:=\:\frac{\Delta{p}}{{p}_{\mathrm{1}} }\:.\:\mathrm{100\%}\:=\:\mathrm{41}.\mathrm{4}\:\%\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *