Menu Close

The-line-y-mx-c-touches-ellipse-x-2-a-2-y-2-b-2-1-prove-that-the-foot-of-perpendicular-from-focus-into-this-line-lie-on-auxillary-circle-x-2-y-2-a-2-

Tinku Tara 0 Comments
Pin




Question Number 51590 by peter frank last updated on 28/Dec/18
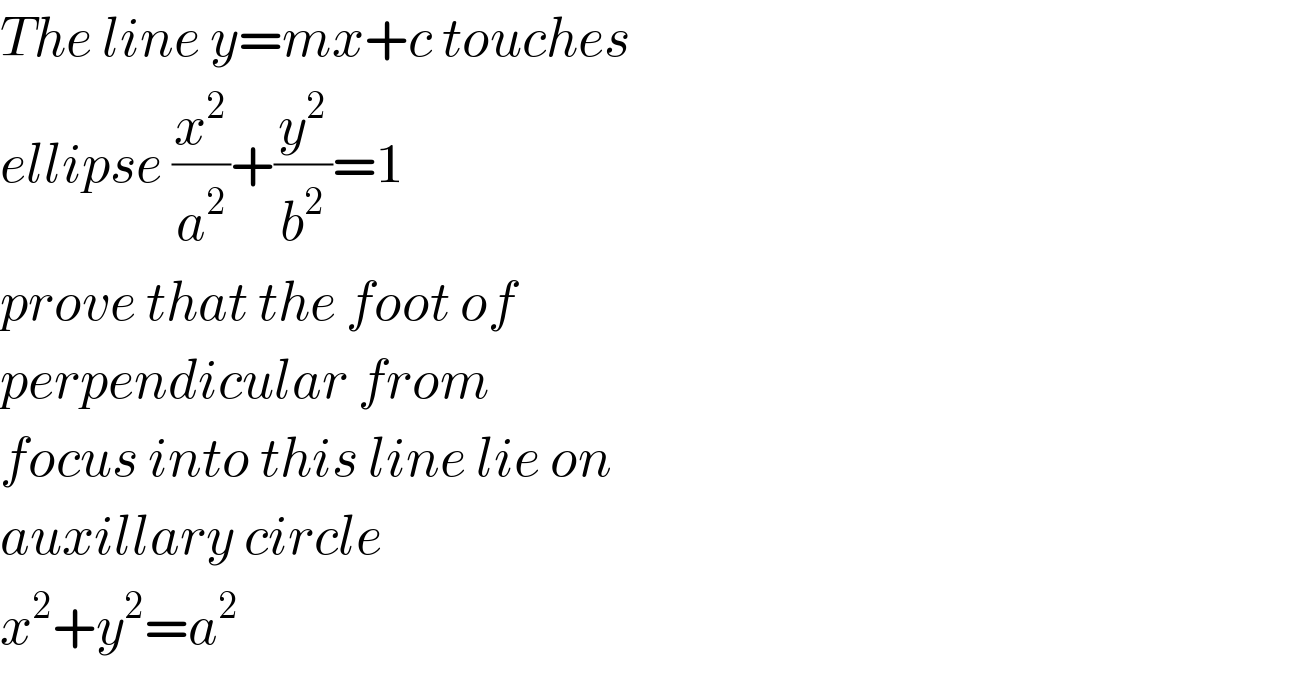
The line y=mx+c touches ellipse (x^2 /a^2 )+(y^2 /b^2 )=1 prove that the foot of perpendicular from focus into this line lie on auxillary circle x^2 +y^2 =a^2
$${The}\:{line}\:{y}={mx}+{c}\:{touches} \\ $$$${ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${prove}\:{that}\:{the}\:{foot}\:{of}\: \\ $$$${perpendicular}\:{from} \\ $$$${focus}\:{into}\:{this}\:{line}\:{lie}\:{on} \\ $$$${auxillary}\:{circle}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$
Commented by Necxx last updated on 28/Dec/18
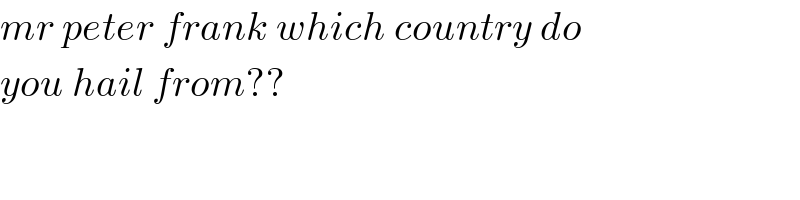
mr peter frank which country do you hail from??
$${mr}\:{peter}\:{frank}\:{which}\:{country}\:{do} \\ $$$${you}\:{hail}\:{from}?? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Dec/18
c^2 =a^2 m^2 +b^2 ← focus(c_1 ,0) and(−c_1 ,0) c_1 ^2 =a^2 −b^2 ← the eqn of st line passing through (c_1 ,0) and ⊥ to y=mx+c is y−0=((−1)/m)(x−c_1 ) y=((−x)/m)+(c_1 /m) solve y=mx+c and y=((−x)/m)+(c_1 /m) to find foot of perpendicular y=mx+c y=((−x)/m)+(c_1 /m) mx+c=((−x)/m)+(c_1 /m) x(m+(1/m))=(c_1 /m)−c x=((c_1 −mc)/(m^2 +1)) so y=m(((c_1 −mc)/(m^2 +1)))+c x=((c_1 −mc)/(m^2 +1)) y=((mc_1 −m^2 c+m^2 c+c)/(m^2 +1)) x^2 +y^2 =((c_1 ^2 −2mcc_1 +m^2 c^2 +m^2 c_1 ^2 +2mcc_1 +c^2 )/((m^2 +1)^2 )) =((c_1 ^2 (m^2 +1)+c^2 (m^2 +1))/((m^2 +1)^2 )) =(((m^2 +1))/((m^2 +1)^2 ))×(c^2 +c_1 ^2 ) =((a^2 m^2 +b^2 +a^2 −b^2 )/((m^2 +1))) =a^2
$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} \leftarrow \\ $$$${focus}\left({c}_{\mathrm{1}} ,\mathrm{0}\right)\:{and}\left(−{c}_{\mathrm{1}} ,\mathrm{0}\right) \\ $$$${c}_{\mathrm{1}} ^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \leftarrow \\ $$$${the}\:{eqn}\:{of}\:{st}\:{line}\:{passing}\:{through}\:\left({c}_{\mathrm{1}} ,\mathrm{0}\right)\:{and} \\ $$$$\bot\:{to}\:{y}={mx}+{c}\:{is} \\ $$$${y}−\mathrm{0}=\frac{−\mathrm{1}}{{m}}\left({x}−{c}_{\mathrm{1}} \right) \\ $$$${y}=\frac{−{x}}{{m}}+\frac{{c}_{\mathrm{1}} }{{m}} \\ $$$${solve}\:{y}={mx}+{c}\:{and}\:{y}=\frac{−{x}}{{m}}+\frac{{c}_{\mathrm{1}} }{{m}}\:{to}\:{find}\:{foot}\:{of} \\ $$$${perpendicular} \\ $$$${y}={mx}+{c} \\ $$$${y}=\frac{−{x}}{{m}}+\frac{{c}_{\mathrm{1}} }{{m}} \\ $$$${mx}+{c}=\frac{−{x}}{{m}}+\frac{{c}_{\mathrm{1}} }{{m}} \\ $$$${x}\left({m}+\frac{\mathrm{1}}{{m}}\right)=\frac{{c}_{\mathrm{1}} }{{m}}−{c} \\ $$$${x}=\frac{{c}_{\mathrm{1}} −{mc}}{{m}^{\mathrm{2}} +\mathrm{1}}\:\:\:{so}\:{y}={m}\left(\frac{{c}_{\mathrm{1}} −{mc}}{{m}^{\mathrm{2}} +\mathrm{1}}\right)+{c} \\ $$$${x}=\frac{{c}_{\mathrm{1}} −{mc}}{{m}^{\mathrm{2}} +\mathrm{1}}\:\:{y}=\frac{{mc}_{\mathrm{1}} −{m}^{\mathrm{2}} {c}+{m}^{\mathrm{2}} {c}+{c}}{{m}^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{mcc}_{\mathrm{1}} +{m}^{\mathrm{2}} {c}^{\mathrm{2}} +{m}^{\mathrm{2}} {c}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}{mcc}_{\mathrm{1}} +{c}^{\mathrm{2}} }{\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)+{c}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)}{\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({m}^{\mathrm{2}} +\mathrm{1}\right)}{\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\left({c}^{\mathrm{2}} +{c}_{\mathrm{1}} ^{\mathrm{2}} \right) \\ $$$$=\frac{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\left({m}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$={a}^{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\: \\ $$
Commented by peter frank last updated on 28/Dec/18
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by peter frank last updated on 28/Dec/18
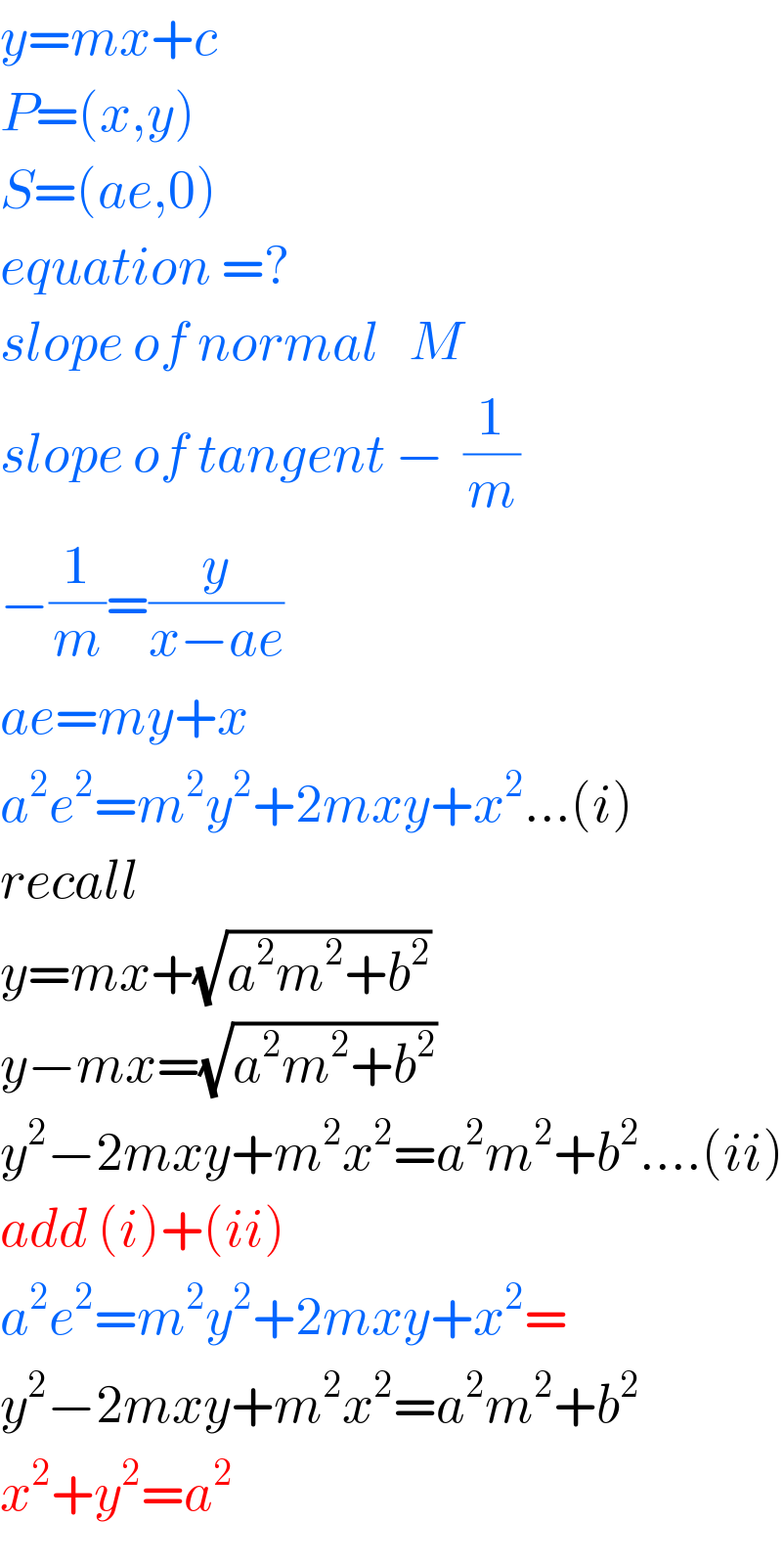
y=mx+c P=(x,y) S=(ae,0) equation =? slope of normal M slope of tangent − (1/m) −(1/m)=(y/(x−ae)) ae=my+x a^2 e^2 =m^2 y^2 +2mxy+x^2 ...(i) recall y=mx+(√(a^2 m^2 +b^2 )) y−mx=(√(a^2 m^2 +b^2 )) y^2 −2mxy+m^2 x^2 =a^2 m^2 +b^2 ....(ii) add (i)+(ii) a^2 e^2 =m^2 y^2 +2mxy+x^2 = y^2 −2mxy+m^2 x^2 =a^2 m^2 +b^2 x^2 +y^2 =a^2
$${y}={mx}+{c} \\ $$$${P}=\left({x},{y}\right) \\ $$$${S}=\left({ae},\mathrm{0}\right) \\ $$$${equation}\:=? \\ $$$${slope}\:{of}\:{normal}\:\:\:{M} \\ $$$${slope}\:{of}\:{tangent}\:−\:\:\frac{\mathrm{1}}{{m}} \\ $$$$−\frac{\mathrm{1}}{{m}}=\frac{{y}}{{x}−{ae}} \\ $$$${ae}={my}+{x} \\ $$$${a}^{\mathrm{2}} {e}^{\mathrm{2}} ={m}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{mxy}+{x}^{\mathrm{2}} …\left({i}\right) \\ $$$${recall} \\ $$$${y}={mx}+\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${y}−{mx}=\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{mxy}+{m}^{\mathrm{2}} {x}^{\mathrm{2}} ={a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} ….\left({ii}\right) \\ $$$${add}\:\left({i}\right)+\left({ii}\right) \\ $$$${a}^{\mathrm{2}} {e}^{\mathrm{2}} ={m}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{mxy}+{x}^{\mathrm{2}} = \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{mxy}+{m}^{\mathrm{2}} {x}^{\mathrm{2}} ={a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *