the-matrice-which-comes-from-the-transformation-matrix-cos-sin-sin-cos-at-90-is-

Question Number 33158 by Rio Mike last updated on 11/Apr/18

t h e m a t r i c e w h i c h c o m e s f r o m

t h e t r a n s f o r m a t i o n m a t r i x

(\begin{matrix} c o s θ - s i n θ \\ s i n θ c o s θ \end{matrix})

a t 90 ° i s ?

Commented by Joel578 last updated on 11/Apr/18

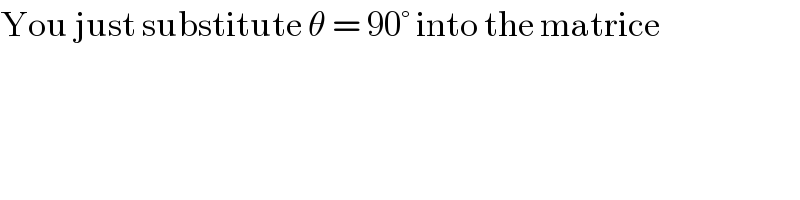
You just substitute θ = 90 ° into the matrice

Commented by prof Abdo imad last updated on 15/Apr/18

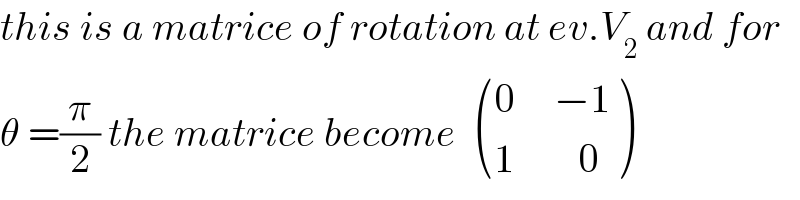
t h i s i s a m a t r i c e o f r o t a t i o n a t e v . V_{2} a n d f o r

θ = \frac{π}{2} t h e m a t r i c e b e c o m e (\begin{matrix} 0 - 1 \\ 1 0 \end{matrix})