Question Number 130054 by EDWIN88 last updated on 22/Jan/21
$$\mathrm{The}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{x}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\mathrm{x}\right)\:\mathrm{is}\:? \\ $$
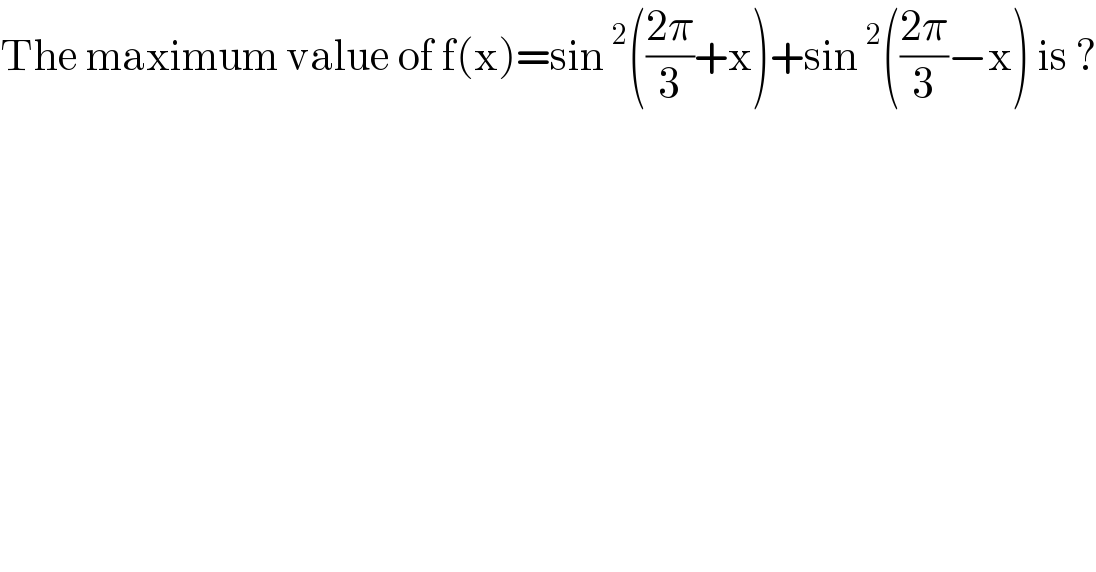
Answered by liberty last updated on 22/Jan/21
Commented by MJS_new last updated on 22/Jan/21
$$\mathrm{0}\leqslant\mathrm{sin}^{\mathrm{2}} \:\alpha\:\leqslant\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant\mathrm{sin}^{\mathrm{2}} \:\alpha\:+\mathrm{sin}^{\mathrm{2}} \:\beta\:\leqslant\mathrm{2} \\ $$$$\mathrm{answer}\:\mathrm{has}\:\mathrm{to}\:\mathrm{be}\:\mathrm{within}\:\mathrm{this}\:\mathrm{interval} \\ $$
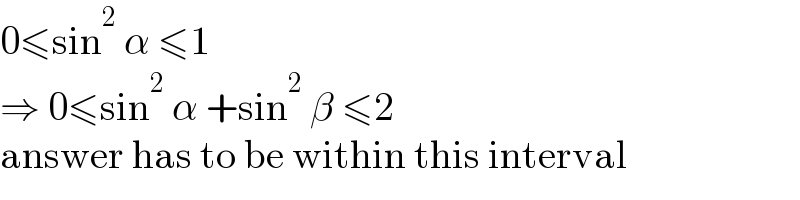
Commented by MJS_new last updated on 22/Jan/21
$$\mathrm{error}\:\mathrm{in}\:\mathrm{line}\:\mathrm{3},\:\mathrm{it}\:\mathrm{musr}\:\mathrm{be}\:−\mathrm{cos}\:\mathrm{2}{x} \\ $$
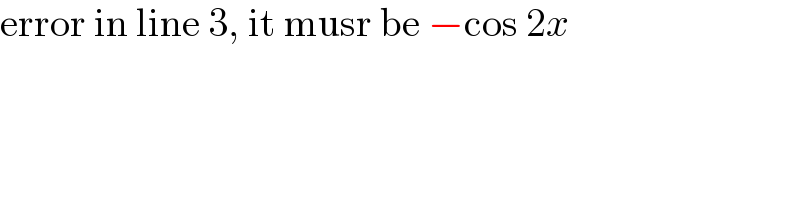
Commented by liberty last updated on 22/Jan/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS_new last updated on 22/Jan/21
![sin^2 (a−x) +sin^2 (a+x) = =(sin a cos x −cos a sin x)^2 +(sin a cos x +cos a sin x)^2 = =2(cos^2 a sin^2 x +2sin^2 a cos^2 x)= =2((1−sin^2 a)sin^2 x +2sin^2 a (1−sin^2 x))= =2(sin^2 a +(1−2sin^2 a)sin^2 x)= [a=((2π)/3)] =(3/2)−sin^2 x (1/2)≤(3/2)−sin^2 x ≤(3/2)](https://www.tinkutara.com/question/Q130058.png)
$$\mathrm{sin}^{\mathrm{2}} \:\left({a}−{x}\right)\:+\mathrm{sin}^{\mathrm{2}} \:\left({a}+{x}\right)\:= \\ $$$$=\left(\mathrm{sin}\:{a}\:\mathrm{cos}\:{x}\:−\mathrm{cos}\:{a}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:{a}\:\mathrm{cos}\:{x}\:+\mathrm{cos}\:{a}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} = \\ $$$$=\mathrm{2}\left(\mathrm{cos}^{\mathrm{2}} \:{a}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:+\mathrm{2sin}^{\mathrm{2}} \:{a}\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)= \\ $$$$=\mathrm{2}\left(\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{a}\right)\mathrm{sin}^{\mathrm{2}} \:{x}\:+\mathrm{2sin}^{\mathrm{2}} \:{a}\:\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}\right)\right)= \\ $$$$=\mathrm{2}\left(\mathrm{sin}^{\mathrm{2}} \:{a}\:+\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{a}\right)\mathrm{sin}^{\mathrm{2}} \:{x}\right)= \\ $$$$\:\:\:\:\:\left[{a}=\frac{\mathrm{2}\pi}{\mathrm{3}}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \:{x}\:\leqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by liberty last updated on 22/Jan/21
$$\mathrm{haha}..\mathrm{what}\:\mathrm{wrong}\:\mathrm{my}\:\mathrm{solution} \\ $$