Menu Close

The-median-AD-of-triangle-ABC-is-bisected-at-E-and-BE-meets-AC-at-F-Find-AF-FC-

Tinku Tara 0 Comments
Pin




Question Number 42180 by rahul 19 last updated on 19/Aug/18
The median AD of triangle ABC is bisected at E and BE meets AC at F. Find AF:FC .
$$\mathrm{The}\:\mathrm{median}\:\mathrm{AD}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{ABC}\:\mathrm{is}\: \\ $$$$\mathrm{bisected}\:\mathrm{at}\:\mathrm{E}\:\mathrm{and}\:\mathrm{BE}\:\mathrm{meets}\:\mathrm{AC}\:\mathrm{at}\:\mathrm{F}. \\ $$$$\mathrm{Find}\:\mathrm{AF}:\mathrm{FC}\:. \\ $$
Answered by MJS last updated on 19/Aug/18
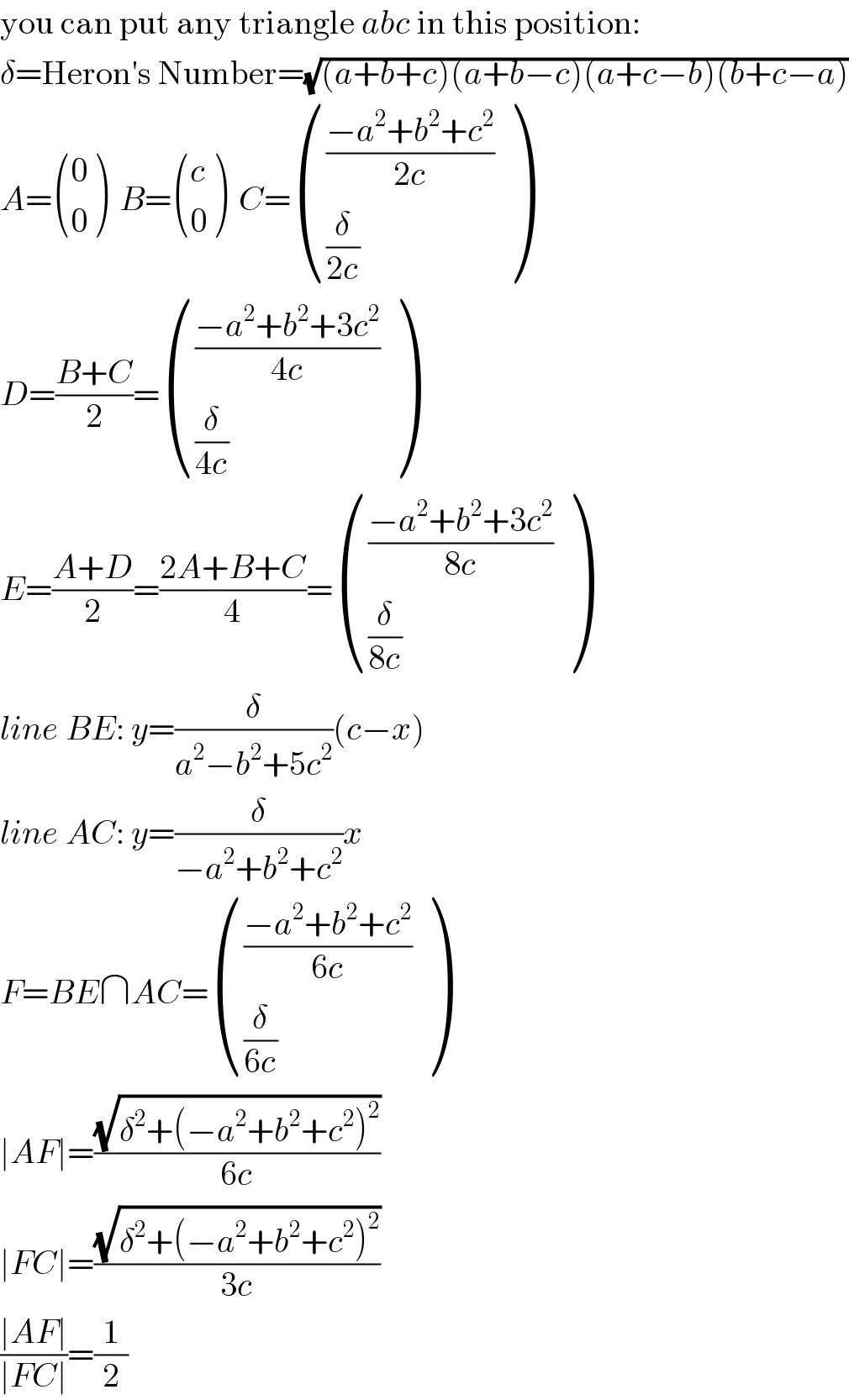
you can put any triangle abc in this position: δ=Heron′s Number=(√((a+b+c)(a+b−c)(a+c−b)(b+c−a))) A= ((0),(0) ) B= ((c),(0) ) C= ((((−a^2 +b^2 +c^2 )/(2c))),((δ/(2c))) ) D=((B+C)/2)= ((((−a^2 +b^2 +3c^2 )/(4c))),((δ/(4c))) ) E=((A+D)/2)=((2A+B+C)/4)= ((((−a^2 +b^2 +3c^2 )/(8c))),((δ/(8c))) ) line BE: y=(δ/(a^2 −b^2 +5c^2 ))(c−x) line AC: y=(δ/(−a^2 +b^2 +c^2 ))x F=BE∩AC= ((((−a^2 +b^2 +c^2 )/(6c))),((δ/(6c))) ) ∣AF∣=((√(δ^2 +(−a^2 +b^2 +c^2 )^2 ))/(6c)) ∣FC∣=((√(δ^2 +(−a^2 +b^2 +c^2 )^2 ))/(3c)) ((∣AF∣)/(∣FC∣))=(1/2)
$$\mathrm{you}\:\mathrm{can}\:\mathrm{put}\:\mathrm{any}\:\mathrm{triangle}\:{abc}\:\mathrm{in}\:\mathrm{this}\:\mathrm{position}: \\ $$$$\delta=\mathrm{Heron}'\mathrm{s}\:\mathrm{Number}=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)} \\ $$$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{c}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{c}}}\\{\frac{\delta}{\mathrm{2}{c}}}\end{pmatrix} \\ $$$${D}=\frac{{B}+{C}}{\mathrm{2}}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{4}{c}}}\\{\frac{\delta}{\mathrm{4}{c}}}\end{pmatrix} \\ $$$${E}=\frac{{A}+{D}}{\mathrm{2}}=\frac{\mathrm{2}{A}+{B}+{C}}{\mathrm{4}}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{8}{c}}}\\{\frac{\delta}{\mathrm{8}{c}}}\end{pmatrix} \\ $$$${line}\:{BE}:\:{y}=\frac{\delta}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{5}{c}^{\mathrm{2}} }\left({c}−{x}\right) \\ $$$${line}\:{AC}:\:{y}=\frac{\delta}{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{x} \\ $$$${F}={BE}\cap{AC}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix} \\ $$$$\mid{AF}\mid=\frac{\sqrt{\delta^{\mathrm{2}} +\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{6}{c}} \\ $$$$\mid{FC}\mid=\frac{\sqrt{\delta^{\mathrm{2}} +\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{3}{c}} \\ $$$$\frac{\mid{AF}\mid}{\mid{FC}\mid}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 20/Aug/18
Sir, how u write coordinates of C?
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{u}\:\mathrm{write}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{C}? \\ $$
Commented by MJS last updated on 20/Aug/18
a=BC b=CA c=AB I put A = point of origin and AB on x−axis ⇒ ⇒ B= ((c),(0) ) to find C we have 2 rectangular triangles c=p+q ⇒ p^2 +h_c ^2 =b^2 ∧ q^2 +h_c ^2 =a^2 C= ((p),(h_c ) ) we know that the area of ABC is (1) ((ch_c )/2) (2) (δ/4) ((ch_c )/2)=(δ/4) ⇒ h_c =(δ/(2c)) p^2 +h_c ^2 =b^2 p^2 =b^2 −h_c ^2 p^2 =((4b^2 c^2 −δ^2 )/(4c^2 )) [δ^2 =2(a^2 b^2 +a^2 c^2 +b^2 c^2 )−(a^4 +b^4 +c^4 )] p^2 =((a^4 +b^4 +c^4 −2a^2 b^2 −2a^2 c^2 +2b^2 c^2 )/(4c^2 )) p^2 =(((−a^2 +b^2 +c^2 )^2 )/(4c^2 )) p=((−a^2 +b^2 +c^2 )/(4c^2 )) C= ((p),(h_c ) ) = ((((−a^2 +b^2 +c^2 )/(4c^2 ))),((δ/(2c))) )
$${a}={BC}\:\:{b}={CA}\:\:{c}={AB} \\ $$$$\mathrm{I}\:\mathrm{put}\:{A}\:=\:\mathrm{point}\:\mathrm{of}\:\mathrm{origin}\:\mathrm{and}\:{AB}\:\mathrm{on}\:{x}−\mathrm{axis}\:\Rightarrow \\ $$$$\Rightarrow\:{B}=\begin{pmatrix}{{c}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{to}\:\mathrm{find}\:{C}\:\mathrm{we}\:\mathrm{have}\:\mathrm{2}\:\mathrm{rectangular}\:\mathrm{triangles} \\ $$$${c}={p}+{q}\:\Rightarrow\:{p}^{\mathrm{2}} +{h}_{{c}} ^{\mathrm{2}} ={b}^{\mathrm{2}} \:\wedge\:{q}^{\mathrm{2}} +{h}_{{c}} ^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${C}=\begin{pmatrix}{{p}}\\{{h}_{{c}} }\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:{ABC}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\frac{{ch}_{{c}} }{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\frac{\delta}{\mathrm{4}} \\ $$$$\frac{{ch}_{{c}} }{\mathrm{2}}=\frac{\delta}{\mathrm{4}}\:\Rightarrow\:{h}_{{c}} =\frac{\delta}{\mathrm{2}{c}} \\ $$$${p}^{\mathrm{2}} +{h}_{{c}} ^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} ={b}^{\mathrm{2}} −{h}_{{c}} ^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} =\frac{\mathrm{4}{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\delta^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\left[\delta^{\mathrm{2}} =\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)\right] \\ $$$${p}^{\mathrm{2}} =\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} {c}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} } \\ $$$${p}^{\mathrm{2}} =\frac{\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} } \\ $$$${p}=\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} } \\ $$$${C}=\begin{pmatrix}{{p}}\\{{h}_{{c}} }\end{pmatrix}\:=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} }}\\{\frac{\delta}{\mathrm{2}{c}}}\end{pmatrix} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *