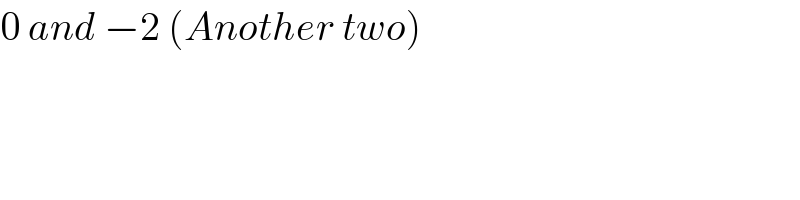The-number-of-integer-values-of-x-satisfying-the-inequality-2x-1-lt-2log-2-x-3-is-

Question Number 121783 by Ar Brandon last updated on 11/Nov/20

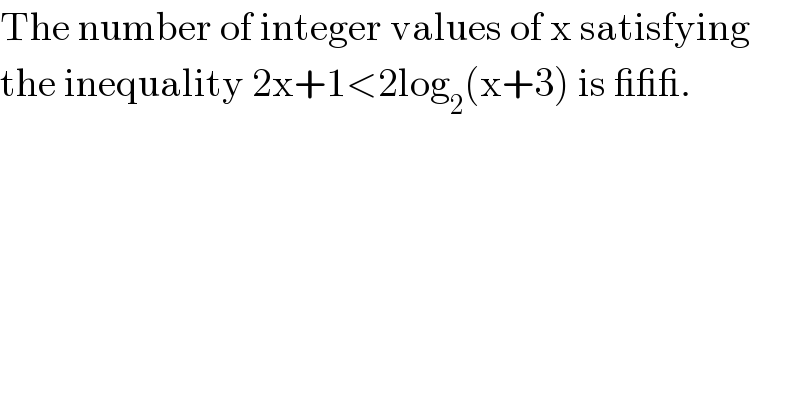
The number of integer values of x satisfying

the inequality 2 x + 1 < {2 \log}_{2} (x + 3) is___.

Answered by TANMAY PANACEA last updated on 11/Nov/20

x = 1 L H S = 3 R H S = 4 R H S > L H S

x = - 1 L H S = - 1 R H S = 2 R H S > L H S

x = 5 L H S = 11 R H S = 6 L H S > R H S

x = 13 L = 27 R = 8 L > R

x = 29 L = 59 R = 10 L > R

s o x = 1 a n d - 1 s a t i s f y t h e e q n

Commented by Ar Brandon last updated on 11/Nov/20

Thanks Sir. But there are 4 integers according to the answer guide.

Commented by Dwaipayan Shikari last updated on 11/Nov/20

0 a n d - 2 (A n o t h e r t w o)