Question Number 121778 by Ar Brandon last updated on 11/Nov/20
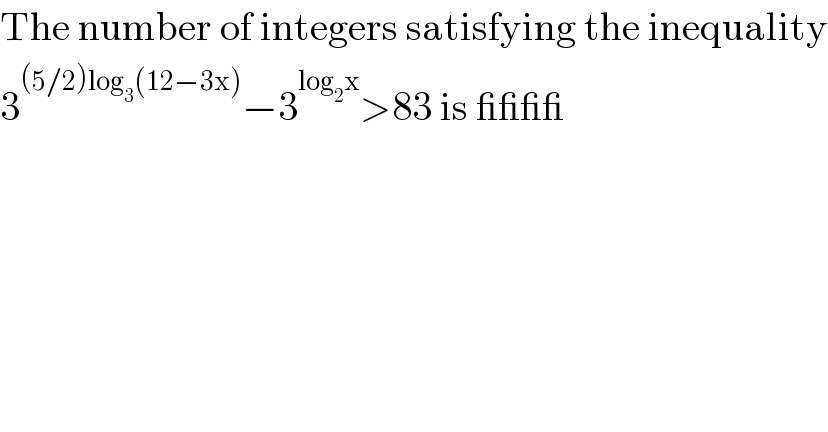
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{integers}\:\mathrm{satisfying}\:\mathrm{the}\:\mathrm{inequality} \\ $$$$\mathrm{3}^{\left(\mathrm{5}/\mathrm{2}\right)\mathrm{log}_{\mathrm{3}} \left(\mathrm{12}−\mathrm{3x}\right)} −\mathrm{3}^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} >\mathrm{83}\:\mathrm{is}\:\_\_\_\_\: \\ $$
Commented by 676597498 last updated on 11/Nov/20
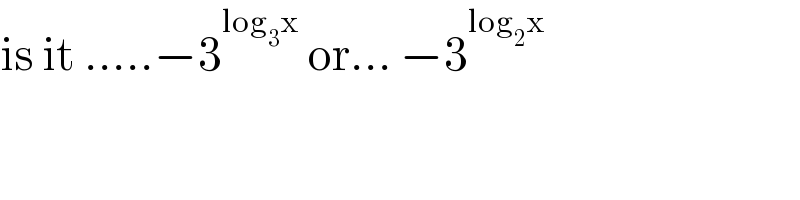
$$\mathrm{is}\:\mathrm{it}\:…..−\mathrm{3}^{\mathrm{log}_{\mathrm{3}} \mathrm{x}} \:\mathrm{or}…\:−\mathrm{3}^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} \\ $$
Commented by Ar Brandon last updated on 11/Nov/20

$$\mathrm{it}'\mathrm{s}\:…−\mathrm{3}^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} \\ $$
Answered by floor(10²Eta[1]) last updated on 11/Nov/20
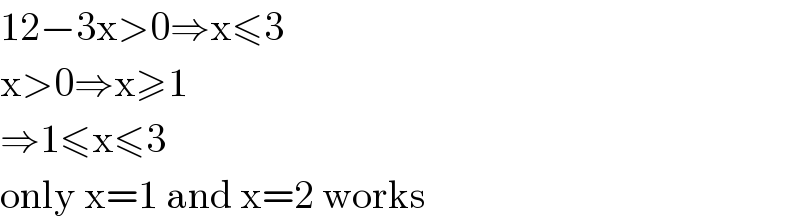
$$\mathrm{12}−\mathrm{3x}>\mathrm{0}\Rightarrow\mathrm{x}\leqslant\mathrm{3} \\ $$$$\mathrm{x}>\mathrm{0}\Rightarrow\mathrm{x}\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{3} \\ $$$$\mathrm{only}\:\mathrm{x}=\mathrm{1}\:\mathrm{and}\:\mathrm{x}=\mathrm{2}\:\mathrm{works} \\ $$
