The-number-of-intersecting-points-on-the-graph-for-sin-x-x-10-for-x-pi-pi-is-

Question Number 16675 by Tinkutara last updated on 25/Jun/17

The number of intersecting points on the graph for sin x = (x/(10)) for x ∈ [−π, π] is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{intersecting}\:\mathrm{points}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{graph}\:\mathrm{for}\:\mathrm{sin}\:{x}\:=\:\frac{{x}}{\mathrm{10}}\:\mathrm{for}\:{x}\:\in\:\left[−\pi,\:\pi\right] \\ $$$$\mathrm{is} \\ $$

Answered by ajfour last updated on 25/Jun/17

Commented by Tinkutara last updated on 25/Jun/17

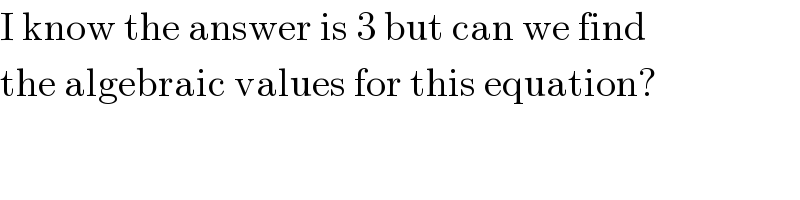
I know the answer is 3 but can we find the algebraic values for this equation?

$$\mathrm{I}\:\mathrm{know}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{3}\:\mathrm{but}\:\mathrm{can}\:\mathrm{we}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{algebraic}\:\mathrm{values}\:\mathrm{for}\:\mathrm{this}\:\mathrm{equation}? \\ $$

Commented by ajfour last updated on 25/Jun/17

y=(x/(10)) barely rises till y=(π/(10)) when x=π . So 3 intersection points for x∈ [−π, π] .

$$\mathrm{y}=\frac{\mathrm{x}}{\mathrm{10}}\:\mathrm{barely}\:\mathrm{rises}\:\mathrm{till}\:\mathrm{y}=\frac{\pi}{\mathrm{10}}\: \\ $$$$\:\mathrm{when}\:\mathrm{x}=\pi\:.\:\mathrm{So}\:\mathrm{3}\:\mathrm{intersection}\: \\ $$$$\:\mathrm{points}\:\mathrm{for}\:\:\mathrm{x}\in\:\left[−\pi,\:\pi\right]\:. \\ $$

Commented by ajfour last updated on 25/Jun/17

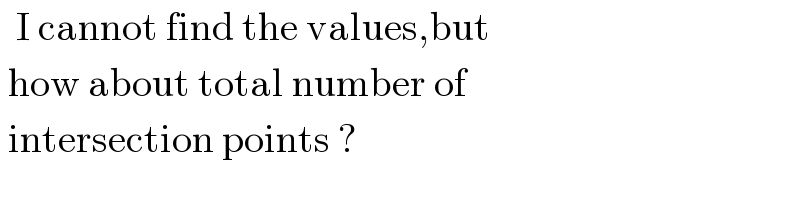
I cannot find the values,but how about total number of intersection points ?

$$\:\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{the}\:\mathrm{values},\mathrm{but} \\ $$$$\:\mathrm{how}\:\mathrm{about}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of} \\ $$$$\:\mathrm{intersection}\:\mathrm{points}\:? \\ $$

Commented by Tinkutara last updated on 25/Jun/17

I don′t have an idea to solve total number of intersection points.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{an}\:\mathrm{idea}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{total} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{points}. \\ $$

Commented by mrW1 last updated on 25/Jun/17

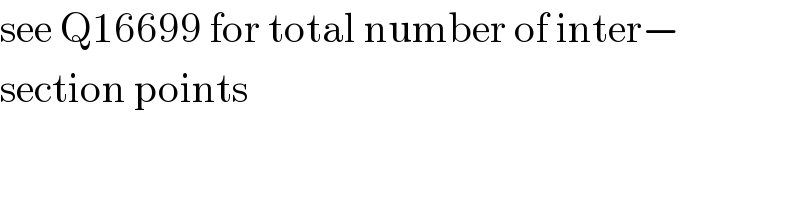
see Q16699 for total number of inter− section points

$$\mathrm{see}\:\mathrm{Q16699}\:\mathrm{for}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{inter}− \\ $$$$\mathrm{section}\:\mathrm{points} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/Jun/17

sinx≅x−(x^3 /6)⇒x−(x^3 /6)=(x/(10))⇒ 60x−10x^3 =6x⇒x(54−10x^2 )=0 ⇒x=0,x=±(√((54)/(10)))=±2.32 ⇒x=0,± 2.32 (equation have 3 answers). there is a little difference between these answers and graphic method. it is not so good,but you can use this way for finding number of answers. for best resualts you can do this with more terms in exprission of ′sinx′.

$${sinx}\cong{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\Rightarrow{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}=\frac{{x}}{\mathrm{10}}\Rightarrow \\ $$$$\mathrm{60}{x}−\mathrm{10}{x}^{\mathrm{3}} =\mathrm{6}{x}\Rightarrow{x}\left(\mathrm{54}−\mathrm{10}{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0},{x}=\pm\sqrt{\frac{\mathrm{54}}{\mathrm{10}}}=\pm\mathrm{2}.\mathrm{32} \\ $$$$\Rightarrow{x}=\mathrm{0},\pm\:\mathrm{2}.\mathrm{32}\:\left({equation}\:{have}\:\mathrm{3}\:{answers}\right). \\ $$$${there}\:{is}\:{a}\:{little}\:{difference}\:{between} \\ $$$${these}\:{answers}\:{and}\:{graphic}\:{method}. \\ $$$${it}\:{is}\:{not}\:{so}\:{good},{but}\:{you}\:{can}\:{use}\:{this} \\ $$$${way}\:{for}\:{finding}\:{number}\:{of}\:{answers}. \\ $$$${for}\:{best}\:{resualts}\:{you}\:{can}\:{do}\:{this}\:{with} \\ $$$${more}\:{terms}\:{in}\:{exprission}\:{of}\:'{sinx}'. \\ $$

Facebook Tweet Pin

The-number-of-intersecting-points-on-the-graph-for-sin-x-x-10-for-x-pi-pi-is-

Leave a Reply Cancel reply