Menu Close

The-number-of-irrational-roots-of-the-equation-x-1-x-2-3x-2-3x-1-21-is-

Tinku Tara 0 Comments
Pin




Question Number 20867 by Tinkutara last updated on 05/Sep/17
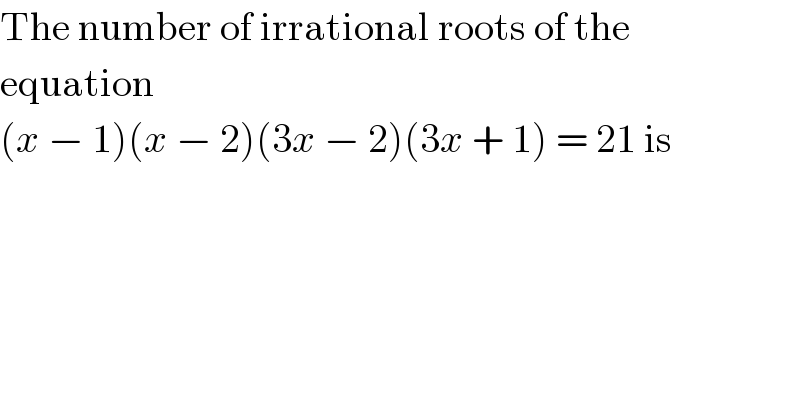
The number of irrational roots of the equation (x − 1)(x − 2)(3x − 2)(3x + 1) = 21 is
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{irrational}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation} \\ $$$$\left({x}\:−\:\mathrm{1}\right)\left({x}\:−\:\mathrm{2}\right)\left(\mathrm{3}{x}\:−\:\mathrm{2}\right)\left(\mathrm{3}{x}\:+\:\mathrm{1}\right)\:=\:\mathrm{21}\:\mathrm{is} \\ $$
Answered by alex041103 last updated on 09/Sep/17
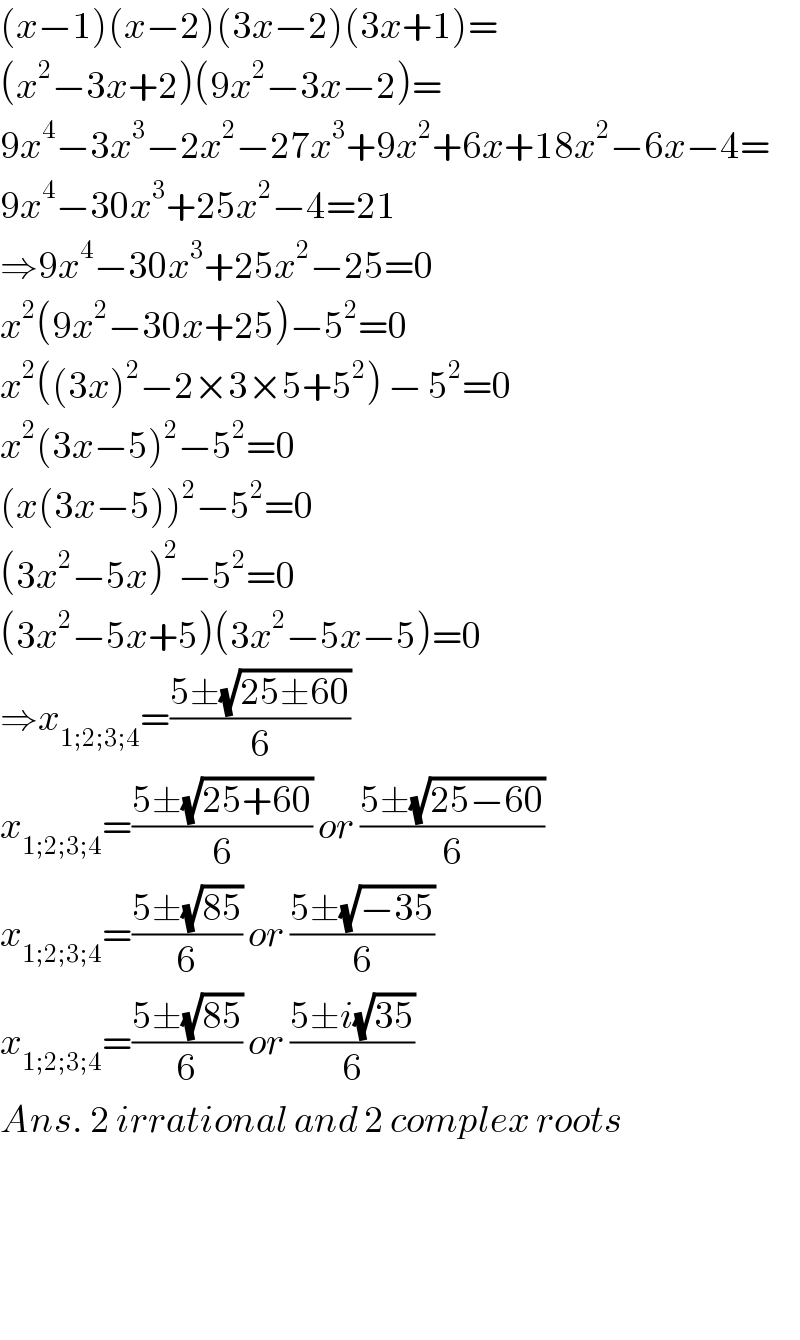
(x−1)(x−2)(3x−2)(3x+1)= (x^2 −3x+2)(9x^2 −3x−2)= 9x^4 −3x^3 −2x^2 −27x^3 +9x^2 +6x+18x^2 −6x−4= 9x^4 −30x^3 +25x^2 −4=21 ⇒9x^4 −30x^3 +25x^2 −25=0 x^2 (9x^2 −30x+25)−5^2 =0 x^2 ((3x)^2 −2×3×5+5^2 ) − 5^2 =0 x^2 (3x−5)^2 −5^2 =0 (x(3x−5))^2 −5^2 =0 (3x^2 −5x)^2 −5^2 =0 (3x^2 −5x+5)(3x^2 −5x−5)=0 ⇒x_(1;2;3;4) =((5±(√(25±60)))/6) x_(1;2;3;4) =((5±(√(25+60)))/6) or ((5±(√(25−60)))/6) x_(1;2;3;4) =((5±(√(85)))/6) or ((5±(√(−35)))/6) x_(1;2;3;4) =((5±(√(85)))/6) or ((5±i(√(35)))/6) Ans. 2 irrational and 2 complex roots
$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)\left(\mathrm{3}{x}+\mathrm{1}\right)= \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{9}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{2}\right)= \\ $$$$\mathrm{9}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{27}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{18}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{4}= \\ $$$$\mathrm{9}{x}^{\mathrm{4}} −\mathrm{30}{x}^{\mathrm{3}} +\mathrm{25}{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{21} \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{4}} −\mathrm{30}{x}^{\mathrm{3}} +\mathrm{25}{x}^{\mathrm{2}} −\mathrm{25}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{9}{x}^{\mathrm{2}} −\mathrm{30}{x}+\mathrm{25}\right)−\mathrm{5}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\left(\mathrm{3}{x}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{5}+\mathrm{5}^{\mathrm{2}} \right)\:−\:\mathrm{5}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{3}{x}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}\left(\mathrm{3}{x}−\mathrm{5}\right)\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{5}\right)\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1};\mathrm{2};\mathrm{3};\mathrm{4}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{25}\pm\mathrm{60}}}{\mathrm{6}} \\ $$$${x}_{\mathrm{1};\mathrm{2};\mathrm{3};\mathrm{4}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{25}+\mathrm{60}}}{\mathrm{6}}\:{or}\:\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{60}}}{\mathrm{6}} \\ $$$${x}_{\mathrm{1};\mathrm{2};\mathrm{3};\mathrm{4}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{85}}}{\mathrm{6}}\:{or}\:\frac{\mathrm{5}\pm\sqrt{−\mathrm{35}}}{\mathrm{6}} \\ $$$${x}_{\mathrm{1};\mathrm{2};\mathrm{3};\mathrm{4}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{85}}}{\mathrm{6}}\:{or}\:\frac{\mathrm{5}\pm{i}\sqrt{\mathrm{35}}}{\mathrm{6}} \\ $$$${Ans}.\:\mathrm{2}\:{irrational}\:{and}\:\mathrm{2}\:{complex}\:{roots} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tinkutara last updated on 09/Sep/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *