Question Number 23231 by Tinkutara last updated on 27/Oct/17
![The number of solution(s) of the equation x^3 + x^2 + 4x + 2sinx = 0 in [0, 2π], is/are](https://www.tinkutara.com/question/Q23231.png)
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solution}\left(\mathrm{s}\right)\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{3}} \:+\:{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:+\:\mathrm{2sin}{x}\:=\:\mathrm{0}\:\mathrm{in}\:\left[\mathrm{0},\:\mathrm{2}\pi\right],\:\mathrm{is}/\mathrm{are} \\ $$
Answered by ajfour last updated on 28/Oct/17
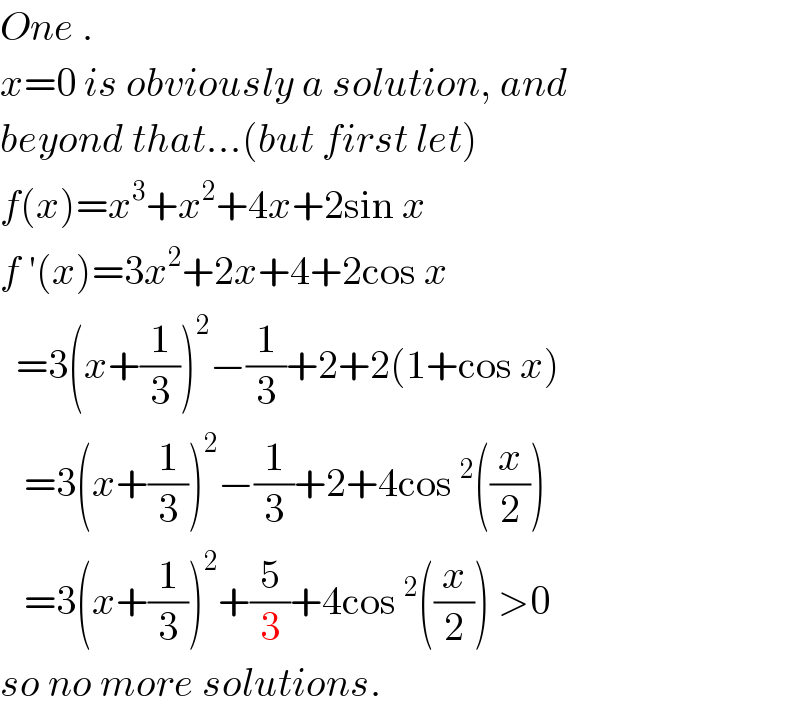
$${One}\:. \\ $$$${x}=\mathrm{0}\:{is}\:{obviously}\:{a}\:{solution},\:{and} \\ $$$${beyond}\:{that}…\left({but}\:{first}\:{let}\right) \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2sin}\:{x} \\ $$$${f}\:'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}+\mathrm{2cos}\:{x} \\ $$$$\:\:=\mathrm{3}\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{2}+\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:{x}\right) \\ $$$$\:\:\:=\mathrm{3}\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{2}+\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\mathrm{3}\left({x}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{3}}+\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:>\mathrm{0} \\ $$$${so}\:{no}\:{more}\:{solutions}. \\ $$
Commented by Tinkutara last updated on 28/Oct/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
