Question Number 16093 by Tinkutara last updated on 17/Jun/17
![The number of solutions of ∣sin x∣ = tan x in [0, 4π] is/are?](https://www.tinkutara.com/question/Q16093.png)
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mid\mathrm{sin}\:{x}\mid\:=\:\mathrm{tan}\:{x}\:\mathrm{in}\:\left[\mathrm{0},\:\mathrm{4}\pi\right]\:\mathrm{is}/\mathrm{are}? \\ $$
Commented by Tinkutara last updated on 17/Jun/17
$$\mathrm{My}\:\mathrm{answer}\:\mathrm{comes}\:\mathrm{out}\:\mathrm{to}\:\mathrm{be}\:\mathrm{5}\:\mathrm{but} \\ $$$$\mathrm{answer}\:\mathrm{in}\:\mathrm{book}\:\mathrm{is}\:\mathrm{6}.\:\mathrm{How}? \\ $$
Commented by prakash jain last updated on 17/Jun/17
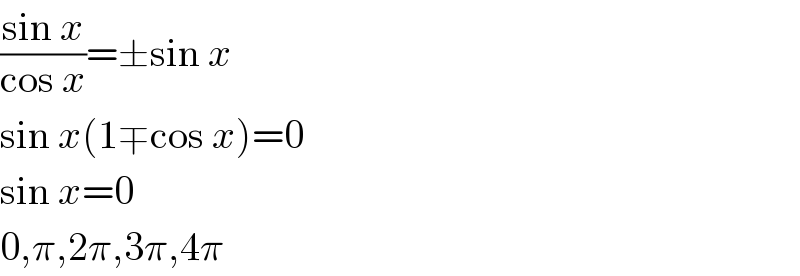
$$\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}=\pm\mathrm{sin}\:{x} \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{1}\mp\mathrm{cos}\:{x}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\mathrm{0},\pi,\mathrm{2}\pi,\mathrm{3}\pi,\mathrm{4}\pi \\ $$
