Menu Close

The-number-of-solutions-of-sin3x-cos2x-0-in-0-3pi-2-is-

Tinku Tara 0 Comments
Pin




Question Number 18545 by Tinkutara last updated on 24/Jul/17
The number of solutions of sin3x + cos2x = 0 in [0, ((3π)/2)] is
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mathrm{sin3}{x}\:+\:\mathrm{cos2}{x}\:=\:\mathrm{0}\:\mathrm{in}\:\left[\mathrm{0},\:\frac{\mathrm{3}\pi}{\mathrm{2}}\right]\:\mathrm{is} \\ $$
Answered by 433 last updated on 24/Jul/17
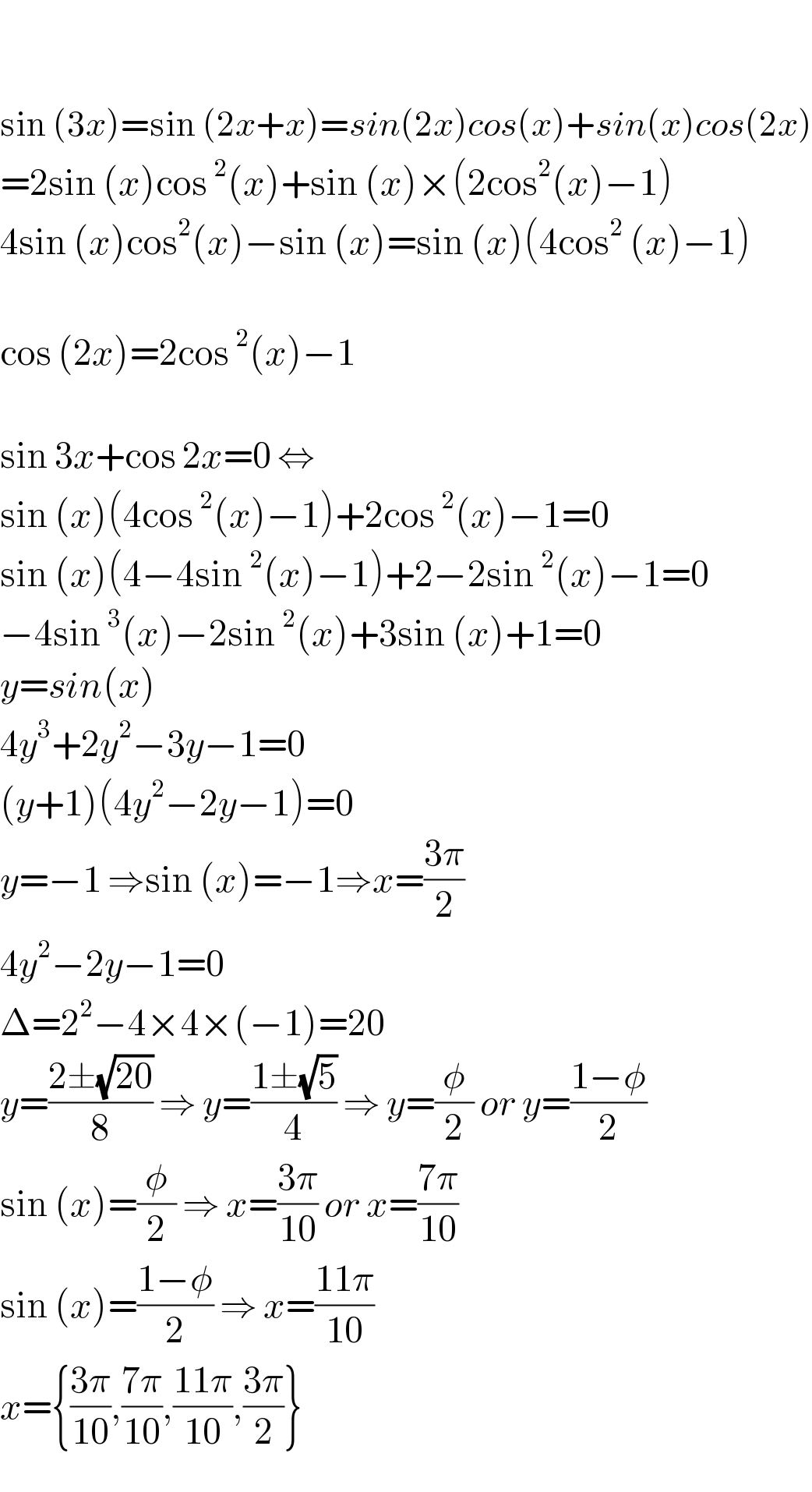
sin (3x)=sin (2x+x)=sin(2x)cos(x)+sin(x)cos(2x) =2sin (x)cos^2 (x)+sin (x)×(2cos^2 (x)−1) 4sin (x)cos^2 (x)−sin (x)=sin (x)(4cos^2 (x)−1) cos (2x)=2cos^2 (x)−1 sin 3x+cos 2x=0 ⇔ sin (x)(4cos^2 (x)−1)+2cos^2 (x)−1=0 sin (x)(4−4sin^2 (x)−1)+2−2sin^2 (x)−1=0 −4sin^3 (x)−2sin^2 (x)+3sin (x)+1=0 y=sin(x) 4y^3 +2y^2 −3y−1=0 (y+1)(4y^2 −2y−1)=0 y=−1 ⇒sin (x)=−1⇒x=((3π)/2) 4y^2 −2y−1=0 Δ=2^2 −4×4×(−1)=20 y=((2±(√(20)))/8) ⇒ y=((1±(√5))/4) ⇒ y=(φ/2) or y=((1−φ)/2) sin (x)=(φ/2) ⇒ x=((3π)/(10)) or x=((7π)/(10)) sin (x)=((1−φ)/2) ⇒ x=((11π)/(10)) x={((3π)/(10)),((7π)/(10)),((11π)/(10)),((3π)/2)}
$$ \\ $$$$ \\ $$$$\mathrm{sin}\:\left(\mathrm{3}{x}\right)=\mathrm{sin}\:\left(\mathrm{2}{x}+{x}\right)={sin}\left(\mathrm{2}{x}\right){cos}\left({x}\right)+{sin}\left({x}\right){cos}\left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{2sin}\:\left({x}\right)\mathrm{cos}\:^{\mathrm{2}} \left({x}\right)+\mathrm{sin}\:\left({x}\right)×\left(\mathrm{2cos}^{\mathrm{2}} \left({x}\right)−\mathrm{1}\right) \\ $$$$\mathrm{4sin}\:\left({x}\right)\mathrm{cos}^{\mathrm{2}} \left({x}\right)−\mathrm{sin}\:\left({x}\right)=\mathrm{sin}\:\left({x}\right)\left(\mathrm{4cos}^{\mathrm{2}} \:\left({x}\right)−\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{x}\right)=\mathrm{2cos}\:^{\mathrm{2}} \left({x}\right)−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{sin}\:\mathrm{3}{x}+\mathrm{cos}\:\mathrm{2}{x}=\mathrm{0}\:\Leftrightarrow \\ $$$$\mathrm{sin}\:\left({x}\right)\left(\mathrm{4cos}\:^{\mathrm{2}} \left({x}\right)−\mathrm{1}\right)+\mathrm{2cos}\:^{\mathrm{2}} \left({x}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}\:\left({x}\right)\left(\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} \left({x}\right)−\mathrm{1}\right)+\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \left({x}\right)−\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{4sin}\:^{\mathrm{3}} \left({x}\right)−\mathrm{2sin}\:^{\mathrm{2}} \left({x}\right)+\mathrm{3sin}\:\left({x}\right)+\mathrm{1}=\mathrm{0} \\ $$$${y}={sin}\left({x}\right) \\ $$$$\mathrm{4}{y}^{\mathrm{3}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\left({y}+\mathrm{1}\right)\left(\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2}{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}=−\mathrm{1}\:\Rightarrow\mathrm{sin}\:\left({x}\right)=−\mathrm{1}\Rightarrow{x}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{2}^{\mathrm{2}} −\mathrm{4}×\mathrm{4}×\left(−\mathrm{1}\right)=\mathrm{20} \\ $$$${y}=\frac{\mathrm{2}\pm\sqrt{\mathrm{20}}}{\mathrm{8}}\:\Rightarrow\:{y}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}}\:\Rightarrow\:{y}=\frac{\phi}{\mathrm{2}}\:{or}\:{y}=\frac{\mathrm{1}−\phi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left({x}\right)=\frac{\phi}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\mathrm{3}\pi}{\mathrm{10}}\:{or}\:{x}=\frac{\mathrm{7}\pi}{\mathrm{10}} \\ $$$$\mathrm{sin}\:\left({x}\right)=\frac{\mathrm{1}−\phi}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\mathrm{11}\pi}{\mathrm{10}} \\ $$$${x}=\left\{\frac{\mathrm{3}\pi}{\mathrm{10}},\frac{\mathrm{7}\pi}{\mathrm{10}},\frac{\mathrm{11}\pi}{\mathrm{10}},\frac{\mathrm{3}\pi}{\mathrm{2}}\right\} \\ $$
Commented by Tinkutara last updated on 24/Jul/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *