Question Number 17421 by Tinkutara last updated on 05/Jul/17
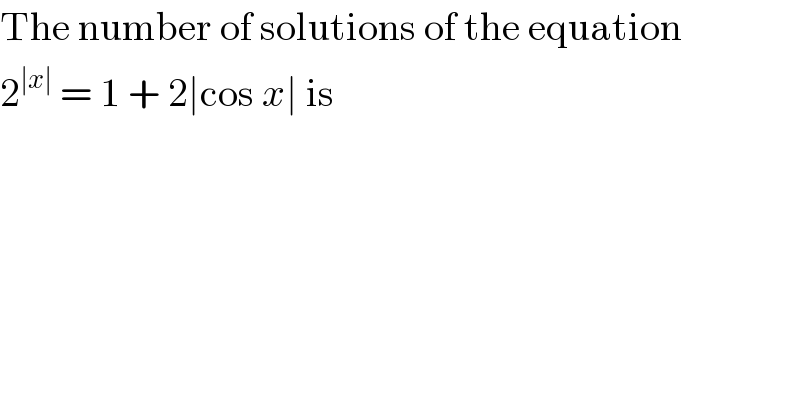
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{2}^{\mid{x}\mid} \:=\:\mathrm{1}\:+\:\mathrm{2}\mid\mathrm{cos}\:{x}\mid\:\mathrm{is} \\ $$
Answered by mrW1 last updated on 05/Jul/17

$$\mathrm{1}\leqslant\:\mathrm{1}\:+\:\mathrm{2}\mid\mathrm{cos}\:{x}\mid\:\leqslant\mathrm{3} \\ $$$$\mathrm{1}\leqslant\:\mathrm{2}^{\mid\mathrm{x}\mid} \:\leqslant\mathrm{3} \\ $$$$\Rightarrow\mathrm{0}\leqslant\mid\mathrm{x}\mid\leqslant\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}\approx\mathrm{1}.\mathrm{58} \\ $$$$\Rightarrow−\mathrm{1}.\mathrm{58}\:\leqslant\mathrm{x}\leqslant\mathrm{1}.\mathrm{58} \\ $$$$\mathrm{at}\:\mathrm{x}=\mathrm{0}: \\ $$$$\mathrm{LHS}=\mathrm{2}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{RHS}=\mathrm{1}+\mathrm{2}=\mathrm{3}>\mathrm{LHS} \\ $$$$\mathrm{at}\:\mathrm{x}=\mathrm{1}.\mathrm{58}: \\ $$$$\mathrm{LHS}=\mathrm{2}^{\mathrm{1}.\mathrm{58}} =\mathrm{2}.\mathrm{99} \\ $$$$\mathrm{RHS}=\mathrm{1}+\mathrm{2}×\mathrm{cos}\:\mathrm{1}.\mathrm{58}=\mathrm{0}.\mathrm{98}<\mathrm{LHS} \\ $$$$\mathrm{since}\:\mathrm{LHS}\:\mathrm{is}\:\mathrm{increasing}\:\mathrm{and}\:\mathrm{RHS}\:\mathrm{is}\:\mathrm{decreasing}, \\ $$$$\mathrm{for}\:\mathrm{0}<\mathrm{x}<\mathrm{1}.\mathrm{58},\:\mathrm{there}\:\mathrm{is}\:\mathrm{one}\:\mathrm{point}\:\mathrm{where} \\ $$$$\mathrm{LHS}=\mathrm{RHS} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\Rightarrow\mathrm{totally}\:\mathrm{2}\:\mathrm{points}\: \\ $$
Commented by Tinkutara last updated on 10/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
