Menu Close

The-number-of-solutions-of-the-equation-cos-1-x-2-1-x-2-1-sin-1-2x-x-2-1-tan-1-2x-x-2-1-2pi-3-

Tinku Tara 0 Comments
Pin




Question Number 44172 by rahul 19 last updated on 22/Sep/18
The number of solutions of the equation cos^(−1) ((x^2 −1)/(x^2 +1)) + sin^(−1) ((2x)/(x^2 +1)) +tan^(−1) ((2x)/(x^2 −1))=((2π)/3).
$${The}\:{number}\:{of}\:{solutions}\:{of}\:{the}\:{equation} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:+\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}\pi}{\mathrm{3}}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Sep/18
Answered by MJS last updated on 22/Sep/18
x=tan (θ/2) ((x^2 −1)/(x^2 +1))=−cos θ ((2x)/(x^2 +1))=sin θ ((2x)/(x^2 −1))=−tan θ but arccos(−cos θ), arcsin(sin θ) and arctan(−tan θ) are strange functions and we get (z∈Z) θ_1 =(π/3)+2πz ⇒ x_1 =((√3)/3) θ_2 =((7π)/9)+2πz ⇒ x_2 =cot (π/9) =tan ((7π)/(18)) θ_3 =((5π)/3)+2πz ⇒ x_3 =−((√3)/3)
$${x}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}=−\mathrm{cos}\:\theta\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{sin}\:\theta\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{1}}=−\mathrm{tan}\:\theta \\ $$$$\mathrm{but}\:\mathrm{arccos}\left(−\mathrm{cos}\:\theta\right),\:\mathrm{arcsin}\left(\mathrm{sin}\:\theta\right)\:\mathrm{and} \\ $$$$\mathrm{arctan}\left(−\mathrm{tan}\:\theta\right)\:\mathrm{are}\:\mathrm{strange}\:\mathrm{functions}\:\mathrm{and} \\ $$$$\mathrm{we}\:\mathrm{get}\:\left({z}\in\mathbb{Z}\right) \\ $$$$\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{3}}+\mathrm{2}\pi{z}\:\Rightarrow\:{x}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\theta_{\mathrm{2}} =\frac{\mathrm{7}\pi}{\mathrm{9}}+\mathrm{2}\pi{z}\:\Rightarrow\:{x}_{\mathrm{2}} =\mathrm{cot}\:\frac{\pi}{\mathrm{9}}\:=\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{18}} \\ $$$$\theta_{\mathrm{3}} =\frac{\mathrm{5}\pi}{\mathrm{3}}+\mathrm{2}\pi{z}\:\Rightarrow\:{x}_{\mathrm{3}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by rahul 19 last updated on 23/Sep/18
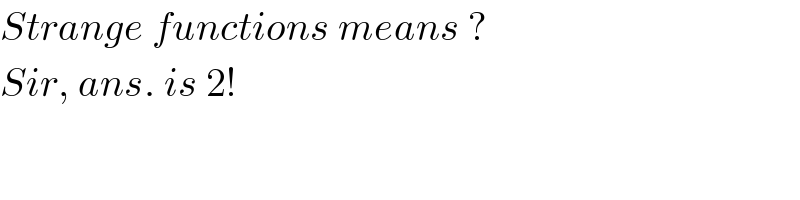
Strange functions means ? Sir, ans. is 2!
$${Strange}\:{functions}\:{means}\:? \\ $$$${Sir},\:{ans}.\:{is}\:\mathrm{2}! \\ $$
Commented by MJS last updated on 23/Sep/18
[0; 2π[ arccos(−cos θ)= { ((π−θ∧θ∈[0; π[)),((θ−π∧θ∈[π; 2π[)) :} arcsin(sin θ)= { ((θ∧θ∈[0; (π/2)[)),((π−θ∧θ∈[(π/2); ((3π)/2)[ )),((θ−2π∧θ∈[((3π)/2); 2π[)) :} arctan(−tan θ)= { ((−θ∧θ∈[0; (π/2)[)),((π−θ∧θ∈[(π/2); ((3π)/2)[)),((2π−θ∧θ∈[((3π)/2); 2π[)) :} arccos(−cos θ)+arcsin(sin θ)+arctan(−tan θ)= = { ((π−θ∧θ∈[0; (π/2)[)),((3(π−θ)∧θ∈[(π/2); π[)),((π−θ∧θ∈[π; ((3π)/2)[)),((θ−π∧θ∈[((3π)/2);2π[)) :} ((2π)/3)=π−θ ⇒ θ=(π/3) ⇒ x=((√3)/3) ((2π)/3)=3(π−θ) ⇒ θ=((7π)/9) ⇒ x=tan ((7π)/(18)) ((2π)/3)=π−θ ⇒ θ=(π/3)∉[π; ((3π)/2)[ ((2π)/3)=θ−π ⇒ θ=((5π)/3) ⇒ x=−((√3)/3)
$$\left[\mathrm{0};\:\mathrm{2}\pi\left[\right.\right. \\ $$$$\mathrm{arccos}\left(−\mathrm{cos}\:\theta\right)=\begin{cases}{\pi−\theta\wedge\theta\in\left[\mathrm{0};\:\pi\left[\right.\right.}\\{\theta−\pi\wedge\theta\in\left[\pi;\:\mathrm{2}\pi\left[\right.\right.}\end{cases} \\ $$$$\mathrm{arcsin}\left(\mathrm{sin}\:\theta\right)=\begin{cases}{\theta\wedge\theta\in\left[\mathrm{0};\:\frac{\pi}{\mathrm{2}}\left[\right.\right.}\\{\pi−\theta\wedge\theta\in\left[\frac{\pi}{\mathrm{2}};\:\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\:\right.\right.}\\{\theta−\mathrm{2}\pi\wedge\theta\in\left[\frac{\mathrm{3}\pi}{\mathrm{2}};\:\mathrm{2}\pi\left[\right.\right.}\end{cases} \\ $$$$\mathrm{arctan}\left(−\mathrm{tan}\:\theta\right)=\begin{cases}{−\theta\wedge\theta\in\left[\mathrm{0};\:\frac{\pi}{\mathrm{2}}\left[\right.\right.}\\{\pi−\theta\wedge\theta\in\left[\frac{\pi}{\mathrm{2}};\:\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\right.\right.}\\{\mathrm{2}\pi−\theta\wedge\theta\in\left[\frac{\mathrm{3}\pi}{\mathrm{2}};\:\mathrm{2}\pi\left[\right.\right.}\end{cases} \\ $$$$\mathrm{arccos}\left(−\mathrm{cos}\:\theta\right)+\mathrm{arcsin}\left(\mathrm{sin}\:\theta\right)+\mathrm{arctan}\left(−\mathrm{tan}\:\theta\right)= \\ $$$$=\begin{cases}{\pi−\theta\wedge\theta\in\left[\mathrm{0};\:\frac{\pi}{\mathrm{2}}\left[\right.\right.}\\{\mathrm{3}\left(\pi−\theta\right)\wedge\theta\in\left[\frac{\pi}{\mathrm{2}};\:\pi\left[\right.\right.}\\{\pi−\theta\wedge\theta\in\left[\pi;\:\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\right.\right.}\\{\theta−\pi\wedge\theta\in\left[\frac{\mathrm{3}\pi}{\mathrm{2}};\mathrm{2}\pi\left[\right.\right.}\end{cases} \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{3}}=\pi−\theta\:\Rightarrow\:\theta=\frac{\pi}{\mathrm{3}}\:\Rightarrow\:{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{3}}=\mathrm{3}\left(\pi−\theta\right)\:\Rightarrow\:\theta=\frac{\mathrm{7}\pi}{\mathrm{9}}\:\Rightarrow\:{x}=\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{18}} \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{3}}=\pi−\theta\:\Rightarrow\:\theta=\frac{\pi}{\mathrm{3}}\notin\left[\pi;\:\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\right.\right. \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{3}}=\theta−\pi\:\Rightarrow\:\theta=\frac{\mathrm{5}\pi}{\mathrm{3}}\:\Rightarrow\:{x}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by MJS last updated on 23/Sep/18
also if you draw the original equation you see the 3 solutions
$$\mathrm{also}\:\mathrm{if}\:\mathrm{you}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation}\:\mathrm{you} \\ $$$$\mathrm{see}\:\mathrm{the}\:\mathrm{3}\:\mathrm{solutions} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *