Question Number 20001 by Tinkutara last updated on 20/Aug/17
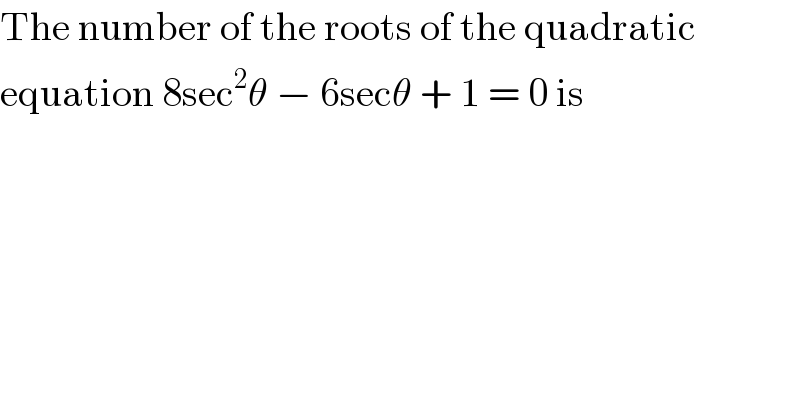
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic} \\ $$$$\mathrm{equation}\:\mathrm{8sec}^{\mathrm{2}} \theta\:−\:\mathrm{6sec}\theta\:+\:\mathrm{1}\:=\:\mathrm{0}\:\mathrm{is} \\ $$
Answered by mrW1 last updated on 20/Aug/17
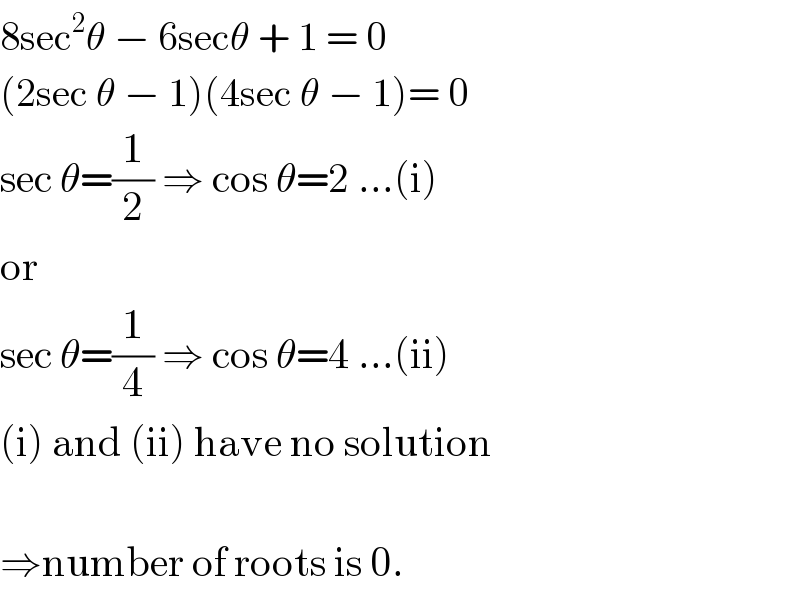
$$\mathrm{8sec}^{\mathrm{2}} \theta\:−\:\mathrm{6sec}\theta\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2sec}\:\theta\:−\:\mathrm{1}\right)\left(\mathrm{4sec}\:\theta\:−\:\mathrm{1}\right)=\:\mathrm{0} \\ $$$$\mathrm{sec}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{cos}\:\theta=\mathrm{2}\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{or} \\ $$$$\mathrm{sec}\:\theta=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{cos}\:\theta=\mathrm{4}\:…\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\:\mathrm{have}\:\mathrm{no}\:\mathrm{solution} \\ $$$$ \\ $$$$\Rightarrow\mathrm{number}\:\mathrm{of}\:\mathrm{roots}\:\mathrm{is}\:\mathrm{0}. \\ $$
Commented by Tinkutara last updated on 20/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
