The-number-of-ways-arrangements-of-the-word-MASKARA-with-exactly-2-A-s-are-adjacent-

Question Number 124916 by liberty last updated on 07/Dec/20

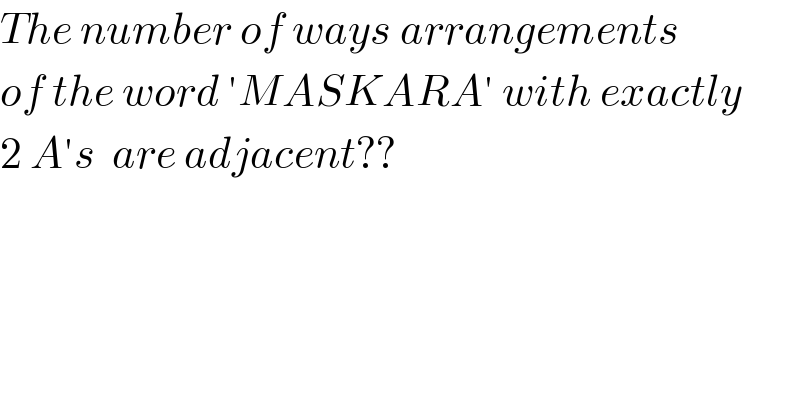
T h e n u m b e r o f w a y s a r r a n g e m e n t s

o f t h e w o r d^{'} {M A S K A R A}^{'} w i t h e x a c t l y

2 A^{'} s a r e a d j a c e n t ? ?

Answered by mr W last updated on 07/Dec/20

_M_S_K_R_

4! \times P_{2}^{5} = 480

Commented by mr W last updated on 07/Dec/20

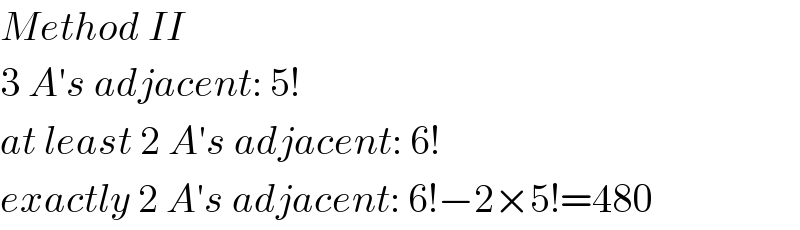
M e t h o d I I

3 A^{'} s a d j a c e n t : 5!

a t l e a s t 2 A^{'} s a d j a c e n t : 6!

e x a c t l y 2 A^{'} s a d j a c e n t : 6! - 2 \times 5! = 480

Commented by bemath last updated on 07/Dec/20

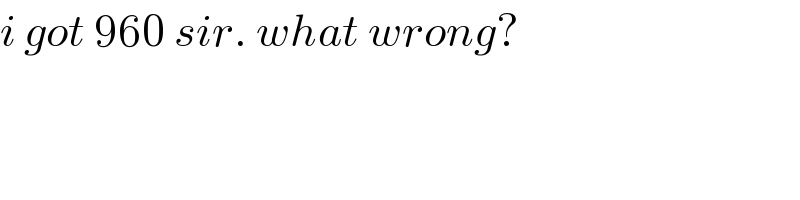
i g o t 960 s i r . w h a t w r o n g ?

Commented by mr W last updated on 07/Dec/20

h o w d i d y o u g e t ?

Answered by liberty last updated on 07/Dec/20

(∙) \underset{1^{s t}}{-} \overset{A A}{-} \underset{2^{n d}}{-} \overset{A}{-} \underset{3^{r d}}{-}

T r e a t 4 l e t t e r s M, S, K, R a s i d e n t i c a l^{'} x^{'}

s i n c e e x a c t l y 2 A^{'} s a r e a d j a c e n t, o n e x m u s t b e

p u t i n 2^{n d} p l a c e s \Rightarrow \underset{1^{s t}}{-} A A \underset{2^{n d}}{\overset{x}{-}} A \underset{3^{r x}}{-}

t h e r e m a i n i n g 3 x^{'} s c a n b e p u t i n (\begin{matrix} 3 + 3 - 1 \\ 3 \end{matrix}) = (\begin{matrix} 5 \\ 3 \end{matrix}) = 10

(∙ ∙) \underset{1^{s t}}{-} A \underset{2^{n d}}{-} A A \underset{3^{r d}}{-} s i m i l a r t o c a s e s (∙)

t h e r e f o r e t h e d e s i r e d n u m b e r o f w a y s

i s g i v e n b y 2 \times (\begin{matrix} 5 \\ 3 \end{matrix}) \times 4! = 20 \times 24 = 480

Facebook Tweet Pin