The-particular-solution-of-differential-equation-of-dy-dx-y-x-k-is-y-1-x-2x-thus-whats-the-value-of-k-

Question Number 103168 by mohammad17 last updated on 13/Jul/20

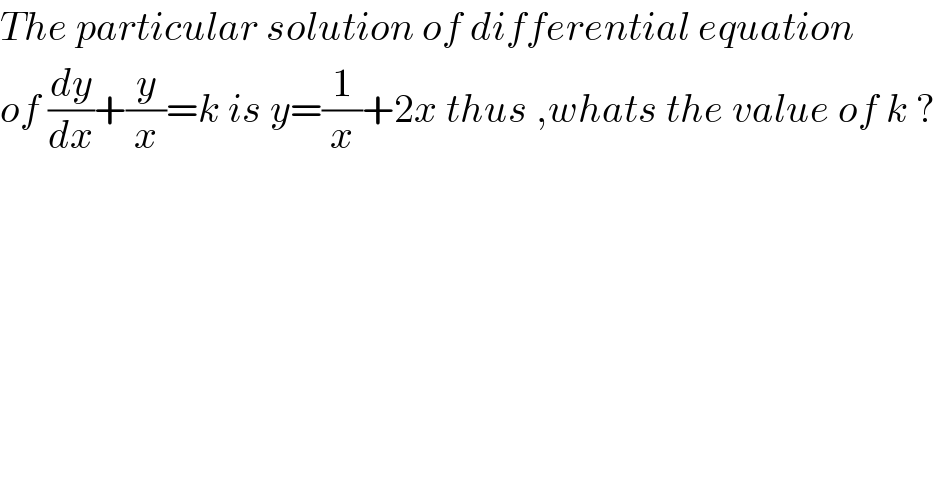
T h e p a r t i c u l a r s o l u t i o n o f d i f f e r e n t i a l e q u a t i o n

o f \frac{d y}{d x} + \frac{y}{x} = k i s y = \frac{1}{x} + 2 x t h u s, w h a t s t h e v a l u e o f k ?

Answered by bemath last updated on 13/Jul/20

I F u (x) = e^{\int \frac{d x}{x}} = e^{\ln (x)} = x

x . \frac{d y}{d x} + y = k x

\frac{d}{d x} (x y) = k x

x y = \frac{1}{2} {k x}^{2} + C

y = \frac{k x}{2} + \frac{C}{x}, t h e n \frac{k x}{2} = 2 x

∴ k = 4

Commented by mohammad17 last updated on 13/Jul/20

t h a n k y o u s i r