Question Number 15086 by Tinkutara last updated on 07/Jun/17
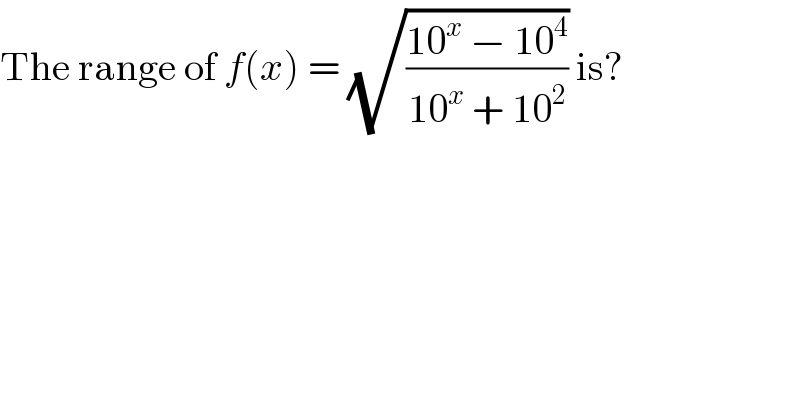
$$\mathrm{The}\:\mathrm{range}\:\mathrm{of}\:{f}\left({x}\right)\:=\:\sqrt{\frac{\mathrm{10}^{{x}} \:−\:\mathrm{10}^{\mathrm{4}} }{\mathrm{10}^{{x}} \:+\:\mathrm{10}^{\mathrm{2}} }}\:\mathrm{is}? \\ $$
Answered by ajfour last updated on 07/Jun/17
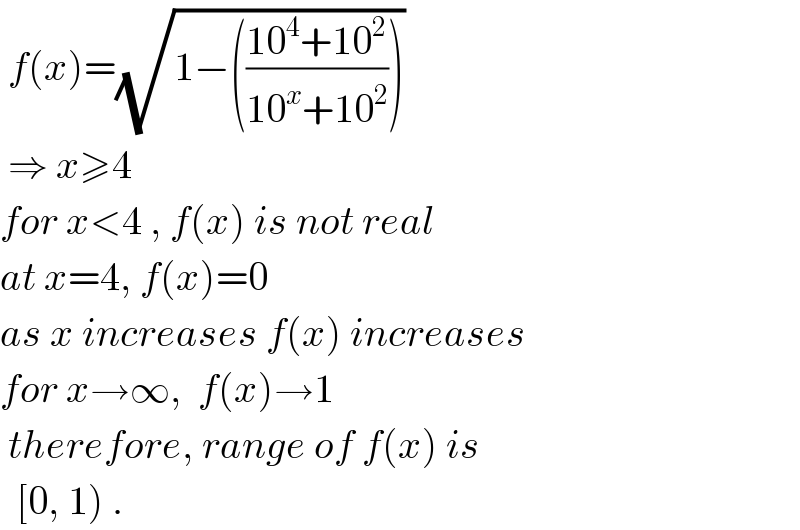
$$\:{f}\left({x}\right)=\sqrt{\mathrm{1}−\left(\frac{\mathrm{10}^{\mathrm{4}} +\mathrm{10}^{\mathrm{2}} }{\mathrm{10}^{{x}} +\mathrm{10}^{\mathrm{2}} }\right)}\: \\ $$$$\:\Rightarrow\:{x}\geqslant\mathrm{4} \\ $$$${for}\:{x}<\mathrm{4}\:,\:{f}\left({x}\right)\:{is}\:{not}\:{real} \\ $$$${at}\:{x}=\mathrm{4},\:{f}\left({x}\right)=\mathrm{0} \\ $$$${as}\:{x}\:{increases}\:{f}\left({x}\right)\:{increases} \\ $$$${for}\:{x}\rightarrow\infty,\:\:{f}\left({x}\right)\rightarrow\mathrm{1} \\ $$$$\:{therefore},\:{range}\:{of}\:{f}\left({x}\right)\:{is} \\ $$$$\:\:\left[\mathrm{0},\:\mathrm{1}\right)\:. \\ $$
Commented by Tinkutara last updated on 07/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
