Question Number 50915 by peter frank last updated on 22/Dec/18

$${The}\:{range}\:{of}\:{riffle}\:{bullet} \\ $$$${is}\:\mathrm{1000}{m}\:{when}\:\theta\:{is}\:{the}\:{angle} \\ $$$${of}\:{projection}.{if}\:{the}\:{bullet} \\ $$$${is}\:{fired}\:\:{with}\:{the}\:{same}\: \\ $$$${angle}\:\:{from}\:{a}\:{car}\:{travelling} \\ $$$${at}\:\mathrm{36}{km}/{h}\:{towards}\:{the}\:{target} \\ $$$${show}\:{that}\:{the}\:{range}\:{will} \\ $$$${be}\:{increased}\:{by} \\ $$$$\frac{\mathrm{1000}}{\mathrm{7}}.\sqrt{{tan}\theta}\:{m}. \\ $$
Answered by mr W last updated on 22/Dec/18
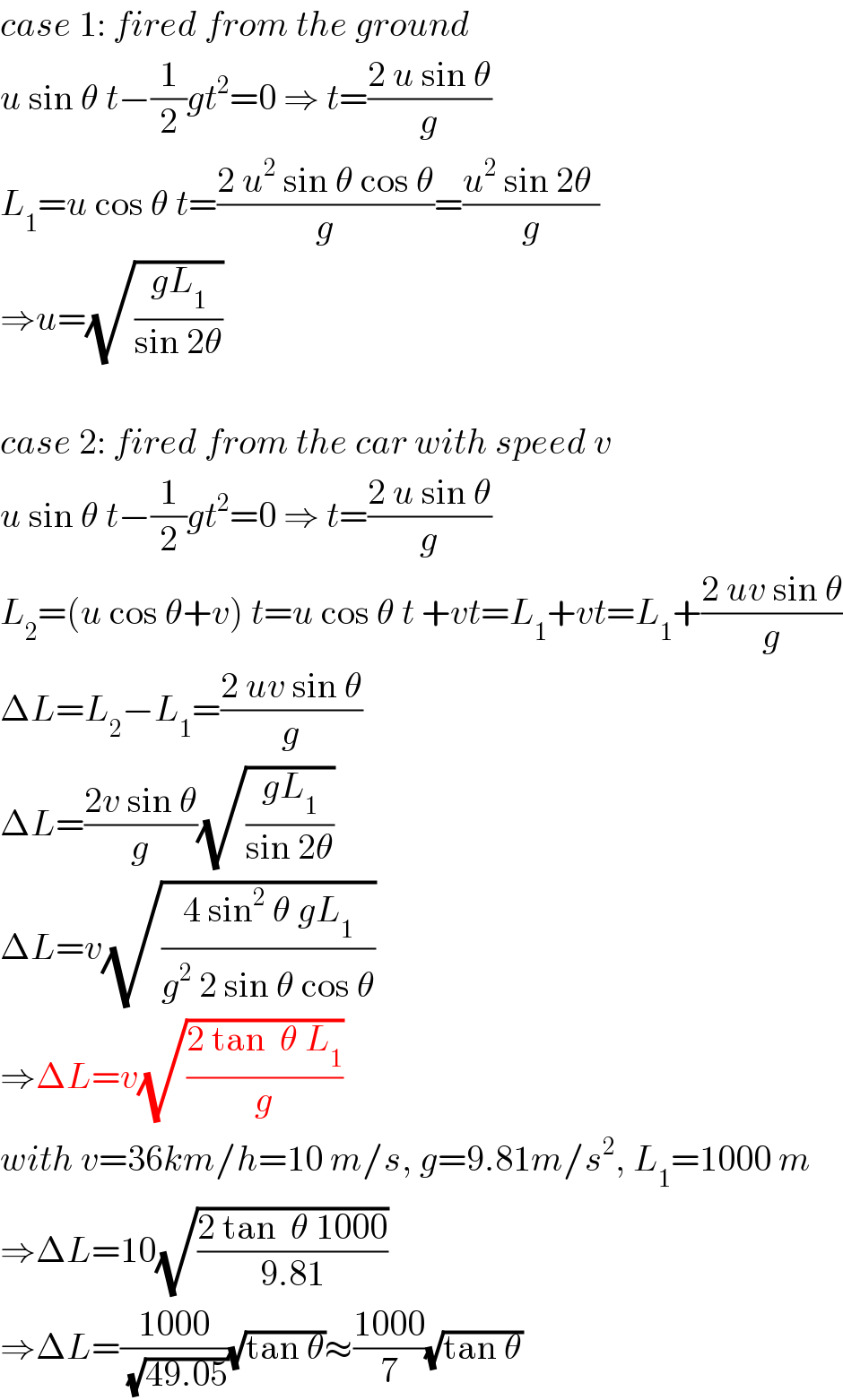
$${case}\:\mathrm{1}:\:{fired}\:{from}\:{the}\:{ground} \\ $$$${u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{t}=\frac{\mathrm{2}\:{u}\:\mathrm{sin}\:\theta}{{g}} \\ $$$${L}_{\mathrm{1}} ={u}\:\mathrm{cos}\:\theta\:{t}=\frac{\mathrm{2}\:{u}^{\mathrm{2}} \:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{{g}}=\frac{{u}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\theta\:}{{g}} \\ $$$$\Rightarrow{u}=\sqrt{\frac{{gL}_{\mathrm{1}} }{\mathrm{sin}\:\mathrm{2}\theta}} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{fired}\:{from}\:{the}\:{car}\:{with}\:{speed}\:{v} \\ $$$${u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{t}=\frac{\mathrm{2}\:{u}\:\mathrm{sin}\:\theta}{{g}} \\ $$$${L}_{\mathrm{2}} =\left({u}\:\mathrm{cos}\:\theta+{v}\right)\:{t}={u}\:\mathrm{cos}\:\theta\:{t}\:+{vt}={L}_{\mathrm{1}} +{vt}={L}_{\mathrm{1}} +\frac{\mathrm{2}\:{uv}\:\mathrm{sin}\:\theta}{{g}} \\ $$$$\Delta{L}={L}_{\mathrm{2}} −{L}_{\mathrm{1}} =\frac{\mathrm{2}\:{uv}\:\mathrm{sin}\:\theta}{{g}} \\ $$$$\Delta{L}=\frac{\mathrm{2}{v}\:\mathrm{sin}\:\theta}{{g}}\sqrt{\frac{{gL}_{\mathrm{1}} }{\mathrm{sin}\:\mathrm{2}\theta}} \\ $$$$\Delta{L}={v}\sqrt{\frac{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\theta\:{gL}_{\mathrm{1}} }{{g}^{\mathrm{2}} \:\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}} \\ $$$$\Rightarrow\Delta{L}={v}\sqrt{\frac{\mathrm{2}\:\mathrm{tan}\:\:\theta\:{L}_{\mathrm{1}} }{{g}}} \\ $$$${with}\:{v}=\mathrm{36}{km}/{h}=\mathrm{10}\:{m}/{s},\:{g}=\mathrm{9}.\mathrm{81}{m}/{s}^{\mathrm{2}} ,\:{L}_{\mathrm{1}} =\mathrm{1000}\:{m} \\ $$$$\Rightarrow\Delta{L}=\mathrm{10}\sqrt{\frac{\mathrm{2}\:\mathrm{tan}\:\:\theta\:\mathrm{1000}}{\mathrm{9}.\mathrm{81}}} \\ $$$$\Rightarrow\Delta{L}=\frac{\mathrm{1000}}{\:\sqrt{\mathrm{49}.\mathrm{05}}}\sqrt{\mathrm{tan}\:\theta}\approx\frac{\mathrm{1000}}{\mathrm{7}}\sqrt{\mathrm{tan}\:\theta} \\ $$
Commented by peter frank last updated on 22/Dec/18

$${thank}\:{you} \\ $$
