Question Number 24772 by Tinkutara last updated on 25/Nov/17
![The ratio of acceleration of points A, B and C is [assume all surfaces are smooth, pulley and strings are light]](https://www.tinkutara.com/question/Q24772.png)
Commented by Tinkutara last updated on 25/Nov/17
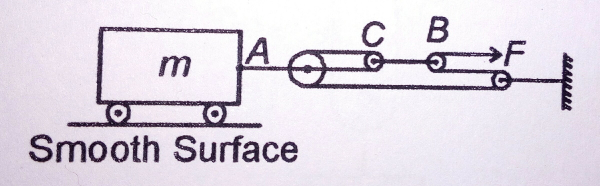
Commented by mrW1 last updated on 26/Nov/17
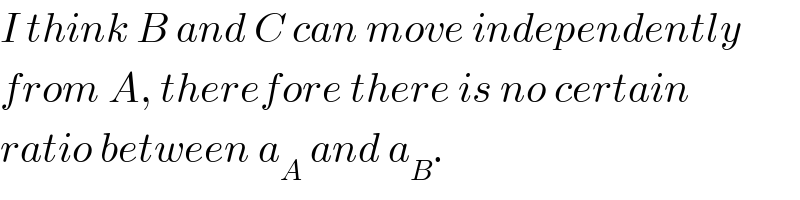
Commented by Tinkutara last updated on 26/Nov/17
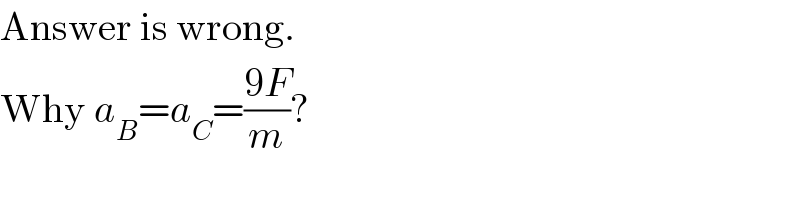
Commented by mrW1 last updated on 26/Nov/17

Commented by Tinkutara last updated on 26/Nov/17
Commented by mrW1 last updated on 26/Nov/17
Commented by ajfour last updated on 26/Nov/17

Commented by mrW1 last updated on 26/Nov/17

Commented by ajfour last updated on 26/Nov/17
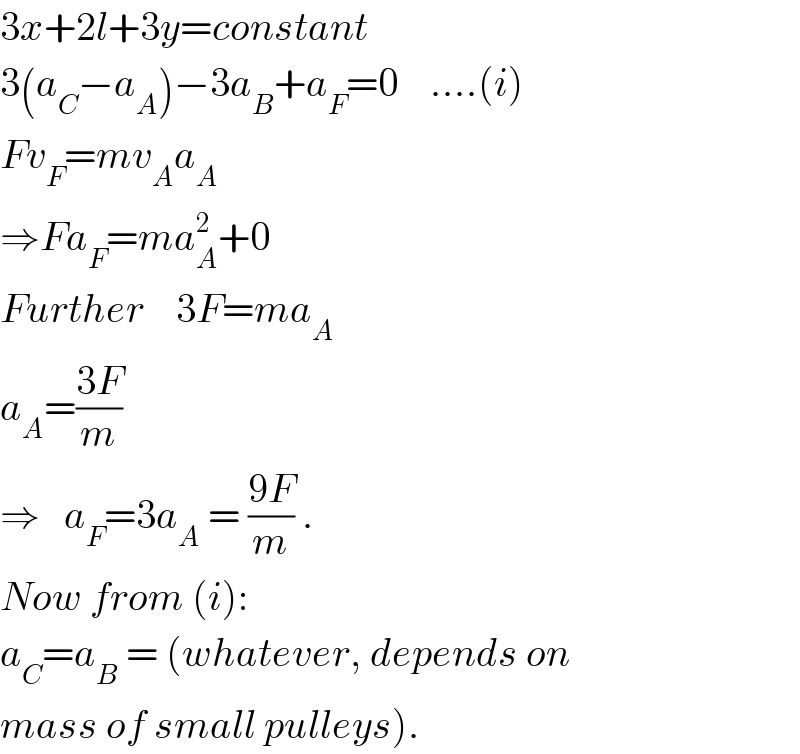
Commented by Tinkutara last updated on 26/Nov/17

Commented by jota+ last updated on 26/Nov/17
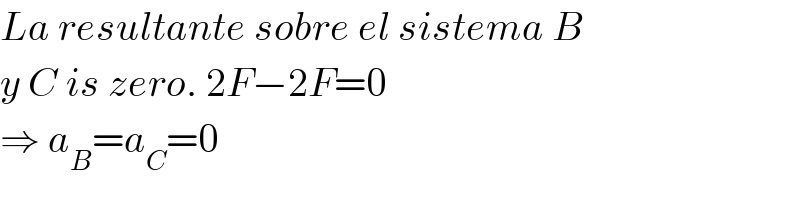
Commented by mrW1 last updated on 26/Nov/17

Commented by Tinkutara last updated on 26/Nov/17