Question Number 169159 by SLVR last updated on 25/Apr/22

$${The}\:{remainder}\:{of} \\ $$$$\mathrm{13}^{\mathrm{13}} {when}\: \\ $$$${divided}\:{by}\:\mathrm{99}\:{is} \\ $$
Commented by SLVR last updated on 25/Apr/22

$${kindly}\:{solve}.. \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 25/Apr/22
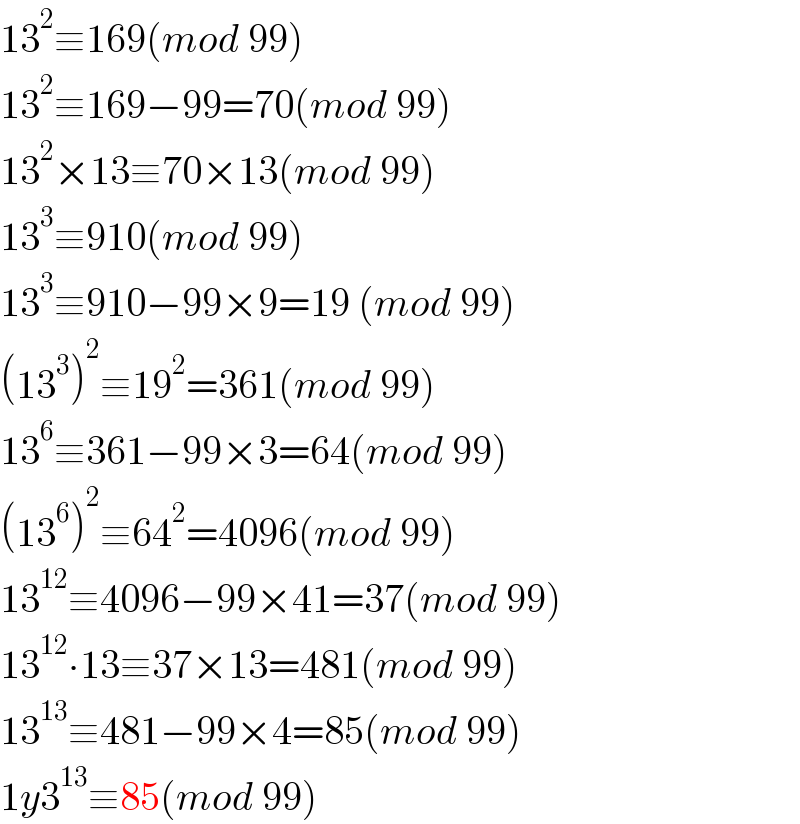
$$\mathrm{13}^{\mathrm{2}} \equiv\mathrm{169}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{2}} \equiv\mathrm{169}−\mathrm{99}=\mathrm{70}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{2}} ×\mathrm{13}\equiv\mathrm{70}×\mathrm{13}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{3}} \equiv\mathrm{910}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{3}} \equiv\mathrm{910}−\mathrm{99}×\mathrm{9}=\mathrm{19}\:\left({mod}\:\mathrm{99}\right) \\ $$$$\left(\mathrm{13}^{\mathrm{3}} \right)^{\mathrm{2}} \equiv\mathrm{19}^{\mathrm{2}} =\mathrm{361}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{6}} \equiv\mathrm{361}−\mathrm{99}×\mathrm{3}=\mathrm{64}\left({mod}\:\mathrm{99}\right) \\ $$$$\left(\mathrm{13}^{\mathrm{6}} \right)^{\mathrm{2}} \equiv\mathrm{64}^{\mathrm{2}} =\mathrm{4096}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{12}} \equiv\mathrm{4096}−\mathrm{99}×\mathrm{41}=\mathrm{37}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{12}} \centerdot\mathrm{13}\equiv\mathrm{37}×\mathrm{13}=\mathrm{481}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{13}} \equiv\mathrm{481}−\mathrm{99}×\mathrm{4}=\mathrm{85}\left({mod}\:\mathrm{99}\right) \\ $$$$\mathrm{1}{y}\mathrm{3}^{\mathrm{13}} \equiv\mathrm{85}\left({mod}\:\mathrm{99}\right) \\ $$
Commented by SLVR last updated on 25/Apr/22

$${So}..{kind}\:{of}\:{you}\:{sir}… \\ $$
