The-reversible-expansion-of-an-ideal-gas-under-adiabatic-and-isothermal-conditions-is-shown-in-the-figure-Which-of-the-following-statement-s-is-are-correct-1-T-1-T-2-2-T-3-gt-T-1-3-

Question Number 24263 by Tinkutara last updated on 14/Nov/17

$$\mathrm{The}\:\mathrm{reversible}\:\mathrm{expansion}\:\mathrm{of}\:\mathrm{an}\:\mathrm{ideal} \\ $$$$\mathrm{gas}\:\mathrm{under}\:\mathrm{adiabatic}\:\mathrm{and}\:\mathrm{isothermal} \\ $$$$\mathrm{conditions}\:\mathrm{is}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the}\:\mathrm{figure}.\:\mathrm{Which} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{statement}\left(\mathrm{s}\right)\:\mathrm{is}\:\left(\mathrm{are}\right) \\ $$$$\mathrm{correct}? \\ $$$$\left(\mathrm{1}\right)\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{T}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{T}_{\mathrm{3}} \:>\:\mathrm{T}_{\mathrm{1}} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{w}_{\mathrm{isothermal}} \:>\:\mathrm{w}_{\mathrm{adiabatic}} \\ $$$$\left(\mathrm{3}\right)\:\Delta\mathrm{U}_{\mathrm{isothermal}} \:>\:\Delta\mathrm{U}_{\mathrm{adiabatic}} \\ $$

Commented by Tinkutara last updated on 14/Nov/17

Commented by ajfour last updated on 14/Nov/17

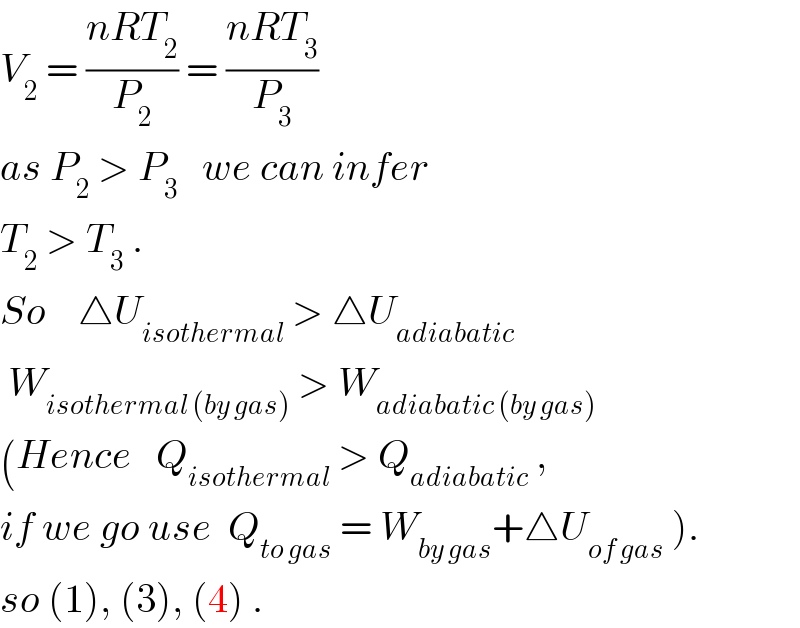
$${V}_{\mathrm{2}} \:=\:\frac{{nRT}_{\mathrm{2}} }{{P}_{\mathrm{2}} }\:=\:\frac{{nRT}_{\mathrm{3}} }{{P}_{\mathrm{3}} } \\ $$$${as}\:{P}_{\mathrm{2}} \:>\:{P}_{\mathrm{3}} \:\:\:{we}\:{can}\:{infer} \\ $$$${T}_{\mathrm{2}} \:>\:{T}_{\mathrm{3}} \:. \\ $$$${So}\:\:\:\:\bigtriangleup{U}_{{isothermal}} \:>\:\bigtriangleup{U}_{{adiabatic}} \\ $$$$\:{W}_{{isothermal}\:\left({by}\:{gas}\right)} \:>\:{W}_{{adiabatic}\:\left({by}\:{gas}\right)} \\ $$$$\left({Hence}\:\:\:{Q}_{{isothermal}} \:>\:{Q}_{{adiabatic}} \:,\right. \\ $$$$\left.{if}\:{we}\:{go}\:{use}\:\:{Q}_{{to}\:{gas}} \:=\:{W}_{{by}\:{gas}} +\bigtriangleup{U}_{{of}\:{gas}} \:\right). \\ $$$${so}\:\left(\mathrm{1}\right),\:\left(\mathrm{3}\right),\:\left(\mathrm{4}\right)\:. \\ $$

Commented by Tinkutara last updated on 15/Nov/17

$$\mathrm{But}\:\mathrm{please}\:\mathrm{recheck}\:\left(\mathrm{2}\right)\:\mathrm{option},\:\mathrm{is}\:\mathrm{it} \\ $$$$\mathrm{true}\:\mathrm{or}\:\mathrm{not}? \\ $$

Commented by ajfour last updated on 15/Nov/17

$${T}_{\mathrm{1}} =\:{T}_{\mathrm{2}} \:\:\:\:{and}\:\:{P}_{\mathrm{2}} \:>\:{P}_{\mathrm{3}} \\ $$$${Also}\:\:\:\:\:\:\frac{{nR}}{{V}_{\mathrm{2}} }\:=\frac{{P}_{\mathrm{2}} }{{T}_{\mathrm{2}} }\:=\:\frac{{P}_{\mathrm{3}} }{{T}_{\mathrm{3}} }\:\:\: \\ $$$$\Rightarrow\:\:{T}_{\mathrm{3}} \:=\:{T}_{\mathrm{2}} \left(\frac{{P}_{\mathrm{3}} }{{P}_{\mathrm{2}} }\right)\:<\:{T}_{\mathrm{2}} \\ $$$${So}\:\:\:\:\:{T}_{\mathrm{3}} \:<\:{T}_{\mathrm{1}} \:. \\ $$

Commented by Tinkutara last updated on 15/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com