Question Number 31933 by NECx last updated on 17/Mar/18
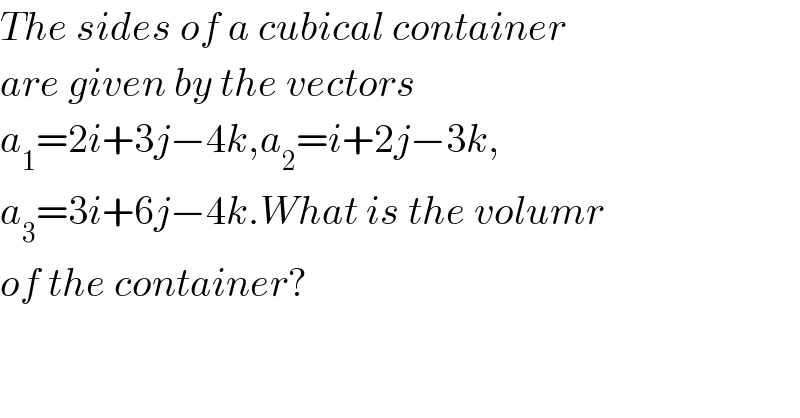
$${The}\:{sides}\:{of}\:{a}\:{cubical}\:{container} \\ $$$${are}\:{given}\:{by}\:{the}\:{vectors} \\ $$$${a}_{\mathrm{1}} =\mathrm{2}{i}+\mathrm{3}{j}−\mathrm{4}{k},{a}_{\mathrm{2}} ={i}+\mathrm{2}{j}−\mathrm{3}{k}, \\ $$$${a}_{\mathrm{3}} =\mathrm{3}{i}+\mathrm{6}{j}−\mathrm{4}{k}.{What}\:{is}\:{the}\:{volumr} \\ $$$${of}\:{the}\:{container}? \\ $$
Answered by JDamian last updated on 17/Mar/18
![V=∣a_1 •(a_2 ×a_3 )∣=∣det [(a_(1x) ,a_(1y) ,a_(1z) ),(a_(2x) ,a_(2y) ,a_(2z) ),(a_(3x) ,a_(3y) ,a_(3z) ) ]∣=∣det [(2,3,(−4)),(1,2,(−3)),(3,6,(−4)) ]∣=5](https://www.tinkutara.com/question/Q31939.png)
$${V}=\mid{a}_{\mathrm{1}} \bullet\left({a}_{\mathrm{2}} ×{a}_{\mathrm{3}} \right)\mid=\mid{det}\begin{bmatrix}{{a}_{\mathrm{1}{x}} }&{{a}_{\mathrm{1}{y}} }&{{a}_{\mathrm{1}{z}} }\\{{a}_{\mathrm{2}{x}} }&{{a}_{\mathrm{2}{y}} }&{{a}_{\mathrm{2}{z}} }\\{{a}_{\mathrm{3}{x}} }&{{a}_{\mathrm{3}{y}} }&{{a}_{\mathrm{3}{z}} }\end{bmatrix}\mid=\mid{det}\begin{bmatrix}{\mathrm{2}}&{\mathrm{3}}&{−\mathrm{4}}\\{\mathrm{1}}&{\mathrm{2}}&{−\mathrm{3}}\\{\mathrm{3}}&{\mathrm{6}}&{−\mathrm{4}}\end{bmatrix}\mid=\mathrm{5} \\ $$
Commented by NECx last updated on 17/Mar/18

$${Thanks} \\ $$
Commented by NECx last updated on 17/Mar/18
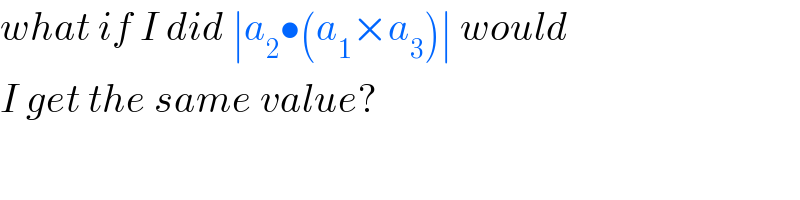
$${what}\:{if}\:{I}\:{did}\:\mid{a}_{\mathrm{2}} \bullet\left({a}_{\mathrm{1}} ×{a}_{\mathrm{3}} \right)\mid\:{would} \\ $$$${I}\:{get}\:{the}\:{same}\:{value}? \\ $$
Commented by JDamian last updated on 18/Mar/18
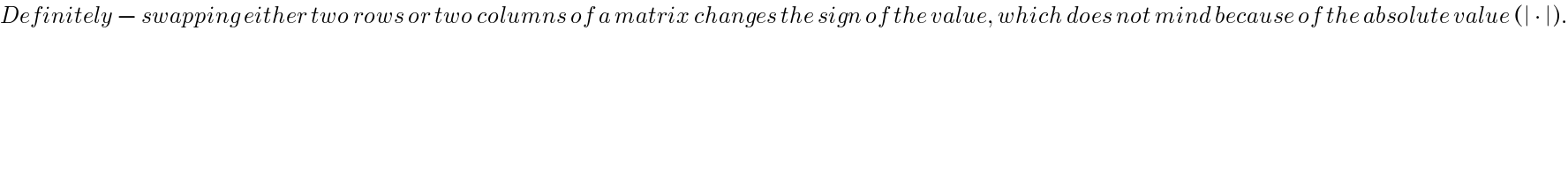
$${Definitely}\:−\:{swapping}\:{either}\:{two}\:{rows}\:{or}\:{two}\:{columns}\:{of}\:{a}\:{matrix}\:{changes}\:{the}\:{sign}\:{of}\:{the}\:{value},\:{which}\:{does}\:{not}\:{mind}\:{because}\:{of}\:{the}\:{absolute}\:{value}\:\left(\mid\:\centerdot\:\mid\right). \\ $$
