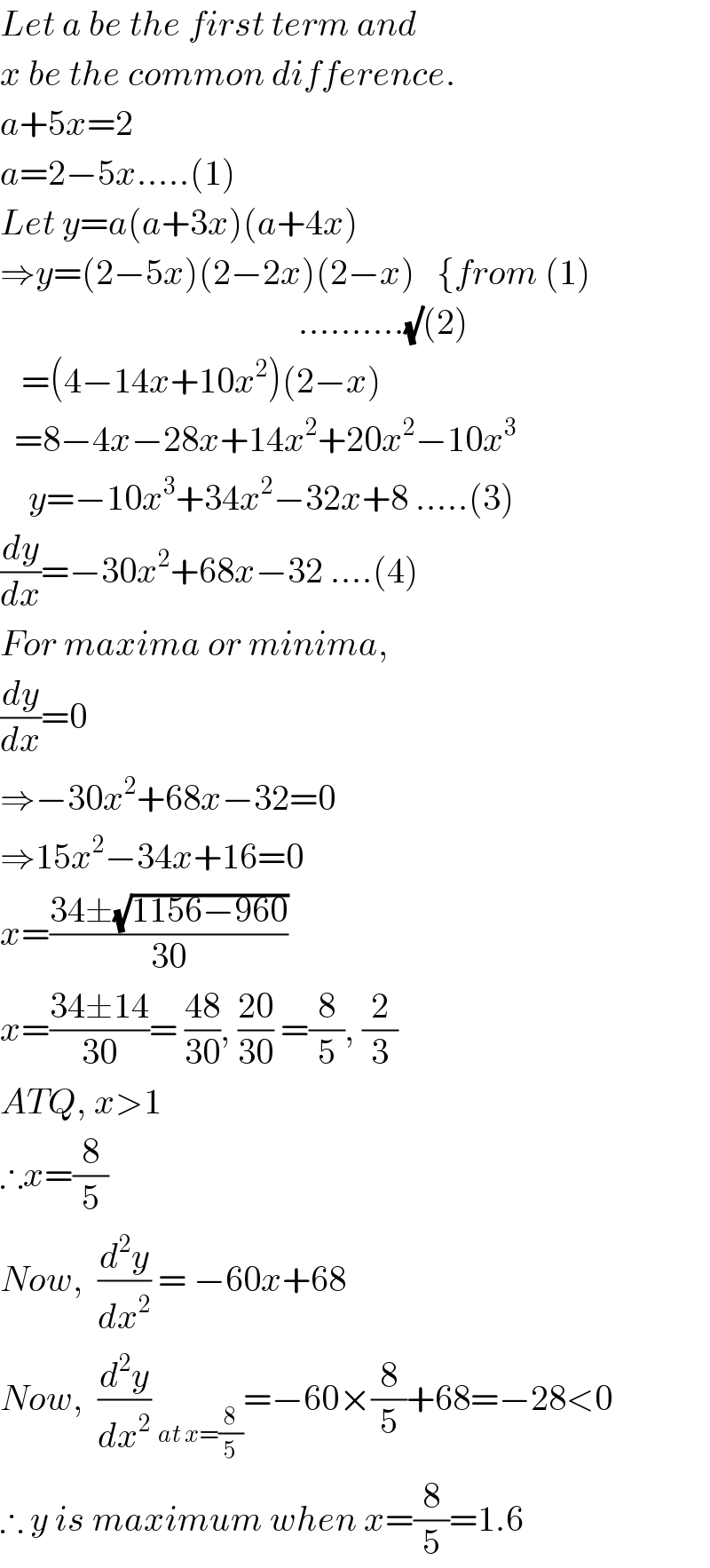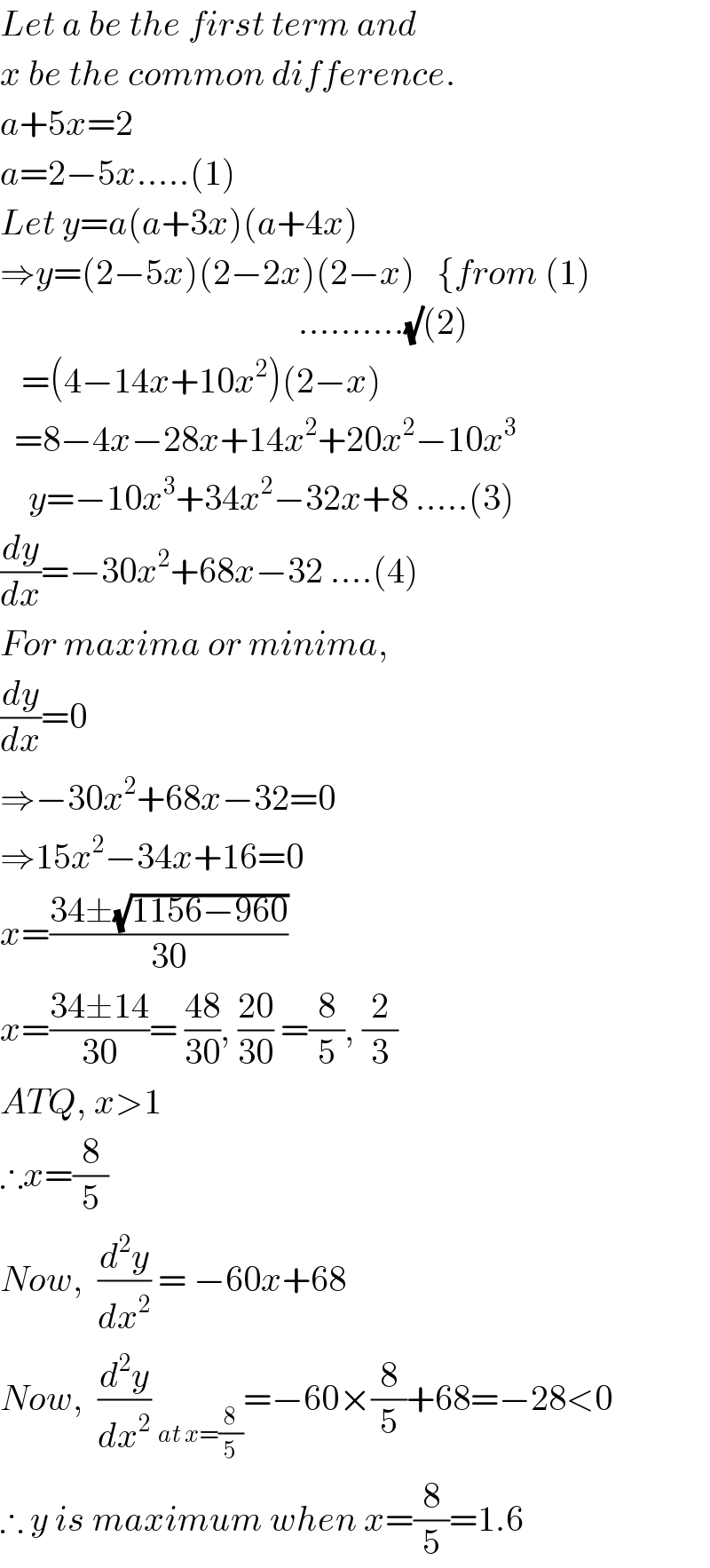The-sixth-term-of-an-A-P-is-2-its-common-difference-is-greater-than-one-Find-the-value-of-the-common-difference-so-that-the-product-of-the-first-fourth-and-fifth-terms-is-the-greatest-

FacebookTweetPin

Question Number 108854 by ZiYangLee last updated on 19/Aug/20

$$\mathrm{The}\mathrm{sixth}\mathrm{term}\mathrm{of}\mathrm{an}\mathrm{A}.\mathrm{P}.\mathrm{is}2,\mathrm{its}$$$$\mathrm{common}\mathrm{difference}\mathrm{is}\mathrm{greater}\mathrm{than}$$$$\mathrm{one}.\mathrm{Find}\mathrm{the}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{common}$$$$\mathrm{difference}\mathrm{so}\mathrm{that}\mathrm{the}\mathrm{product}\mathrm{of}\mathrm{the}$$$$\mathrm{first},\mathrm{fourth}\mathrm{and}\mathrm{fifth}\mathrm{terms}\mathrm{is}\mathrm{the}$$$$\mathrm{greatest}.$$

Answered by $@y@m last updated on 20/Aug/20

$$Letabethefirsttermand$$$$xbethecommondifference.$$$$a+5x=2$$$$a=2-5x\dots ..\left(1\right)$$$$Lety=a(a+3x)(a+4x)$$$$\Rightarrow y=(2-5x)(2-2x)(2-x)\{from\left(1\right)$$$$\dots \dots \dots .\sqrt{}\left(2\right)$$$$=(4-14x+10x^2)(2-x)$$$$=8-4x-28x+14x^2+20x^2-10x^3$$$$y=-10x^3+34x^2-32x+8\dots ..\left(3\right)$$$$\frac{dy}{dx}=-30x^2+68x-32\dots .\left(4\right)$$$$Formaximaorminima,$$$$\frac{dy}{dx}=0$$$$\Rightarrow -30x^2+68x-32=0$$$$\Rightarrow 15x^2-34x+16=0$$$$x=\frac{34\pm \sqrt{1156-960}}{30}$$$$x=\frac{34\pm 14}{30}=\frac{48}{30},\frac{20}{30}=\frac{8}{5},\frac{2}{3}$$$$ATQ,x>1$$$$\therefore x=\frac{8}{5}$$$$Now,\frac{d^{2}y}{{dx}^2}=-60x+68$$$$Now,\frac{d^{2}y}{{dx}^2}{}_{atx=\frac{8}{5}}=-60\times \frac{8}{5}+68=-28<0$$$$\therefore yismaximumwhenx=\frac{8}{5}=1.6$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin