Question Number 130549 by EDWIN88 last updated on 26/Jan/21
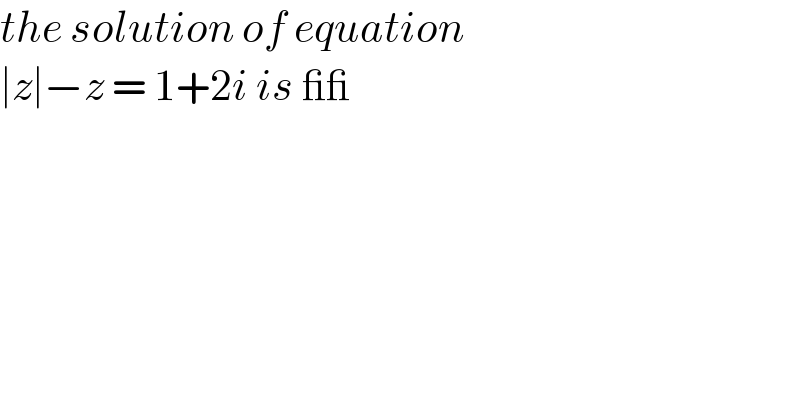
$${the}\:{solution}\:{of}\:{equation}\: \\ $$$$\mid{z}\mid−{z}\:=\:\mathrm{1}+\mathrm{2}{i}\:{is}\:\_\_ \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jan/21
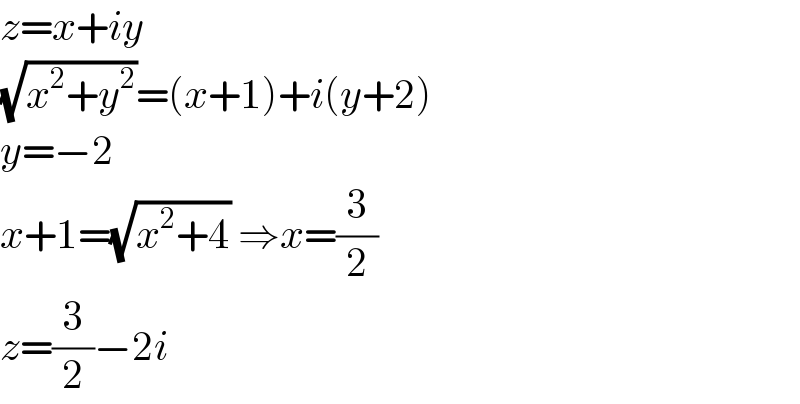
$${z}={x}+{iy} \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\left({x}+\mathrm{1}\right)+{i}\left({y}+\mathrm{2}\right) \\ $$$${y}=−\mathrm{2}\: \\ $$$${x}+\mathrm{1}=\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\:\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${z}=\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2}{i} \\ $$
Answered by liberty last updated on 26/Jan/21

$$\mid\mathrm{z}\mid\:=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\mathrm{x}−\mathrm{y}{i}\:=\mathrm{1}+\mathrm{2}{i} \\ $$$$\begin{cases}{{y}=−\mathrm{2}}\\{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−{x}=\mathrm{1}\:;\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}\:=\:\mathrm{1}+\mathrm{x}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{4}\:=\:\mathrm{1}+\mathrm{2x}+\mathrm{x}^{\mathrm{2}} \:;\:\mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\therefore\:\mathrm{z}\:=\:\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2}{i}\: \\ $$
