Question Number 13654 by Tinkutara last updated on 22/May/17
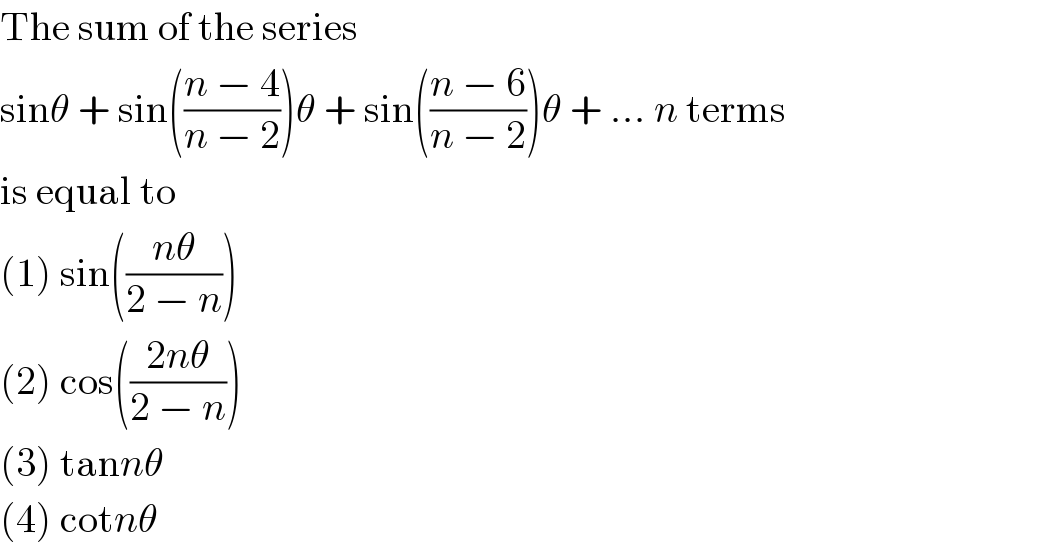
$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$$\mathrm{sin}\theta\:+\:\mathrm{sin}\left(\frac{{n}\:−\:\mathrm{4}}{{n}\:−\:\mathrm{2}}\right)\theta\:+\:\mathrm{sin}\left(\frac{{n}\:−\:\mathrm{6}}{{n}\:−\:\mathrm{2}}\right)\theta\:+\:…\:{n}\:\mathrm{terms} \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{sin}\left(\frac{{n}\theta}{\mathrm{2}\:−\:{n}}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{cos}\left(\frac{\mathrm{2}{n}\theta}{\mathrm{2}\:−\:{n}}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{tan}{n}\theta \\ $$$$\left(\mathrm{4}\right)\:\mathrm{cot}{n}\theta \\ $$
Answered by ajfour last updated on 22/May/17
![T_r =sin (((n−2r)/(n−2)))θ T_(n−1) =sin (((n−2(n−1))/(n−2)))θ=sin (((2−n)/(n−2)))θ T_(n−2) =sin (((n−2(n−2))/(n−2)))θ=sin (((4−n)/(n−2)))θ ..... ..... ..... ..... ...... S = sin (((n−2)/(n−2)))θ+sin (((2−n)/(n−2)))θ +sin (((n−4)/(n−2)))θ+sin (((4−n)/(n−2)))θ +sin (((n−6)/(n−2)))θ+sin (((6−n)/(n−2)))θ + .... + ....... + [+sin (((−n)/(n−2)))θ] excepting the last term, rest all sum to zero. So sum of series = T_n =sin (((nθ)/(2−n))) .](https://www.tinkutara.com/question/Q13662.png)
$$\:{T}_{{r}} =\mathrm{sin}\:\left(\frac{{n}−\mathrm{2}{r}}{{n}−\mathrm{2}}\right)\theta \\ $$$${T}_{{n}−\mathrm{1}} =\mathrm{sin}\:\left(\frac{{n}−\mathrm{2}\left({n}−\mathrm{1}\right)}{{n}−\mathrm{2}}\right)\theta=\mathrm{sin}\:\left(\frac{\mathrm{2}−{n}}{{n}−\mathrm{2}}\right)\theta \\ $$$${T}_{{n}−\mathrm{2}} =\mathrm{sin}\:\left(\frac{{n}−\mathrm{2}\left({n}−\mathrm{2}\right)}{{n}−\mathrm{2}}\right)\theta=\mathrm{sin}\:\left(\frac{\mathrm{4}−{n}}{{n}−\mathrm{2}}\right)\theta \\ $$$$…..\:\:\:\:\:\:…..\:\:\:\:\:…..\:\:\:\:\:…..\:\:\:\:\:…… \\ $$$$\:{S}\:=\:\:\mathrm{sin}\:\left(\frac{{n}−\mathrm{2}}{{n}−\mathrm{2}}\right)\theta+\mathrm{sin}\:\left(\frac{\mathrm{2}−{n}}{{n}−\mathrm{2}}\right)\theta \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{sin}\:\left(\frac{{n}−\mathrm{4}}{{n}−\mathrm{2}}\right)\theta+\mathrm{sin}\:\left(\frac{\mathrm{4}−{n}}{{n}−\mathrm{2}}\right)\theta \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{sin}\:\left(\frac{{n}−\mathrm{6}}{{n}−\mathrm{2}}\right)\theta+\mathrm{sin}\:\left(\frac{\mathrm{6}−{n}}{{n}−\mathrm{2}}\right)\theta \\ $$$$\:\:\:\:\:\:\:\:+\:….\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:……. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\left[+\mathrm{sin}\:\left(\frac{−{n}}{{n}−\mathrm{2}}\right)\theta\right] \\ $$$${excepting}\:{the}\:{last}\:{term},\:{rest} \\ $$$${all}\:{sum}\:{to}\:{zero}. \\ $$$${So}\:{sum}\:{of}\:{series}\:=\:{T}_{{n}} =\mathrm{sin}\:\left(\frac{{n}\theta}{\mathrm{2}−{n}}\right)\:. \\ $$
Commented by Tinkutara last updated on 22/May/17
![But I have calculated it using the formula S_n = ((sin((nβ)/2))/(sin(β/2))) sin[α + (n − 1)(β/2)] where α is the first angle and β is the common difference of the angles which are in AP i.e. to find the sum sinα + sin(α + β) + sin(α + 2β) + ... + sin[α + (n − 1)β]. Using α = θ and (β/2) = (θ/(2 − n)) , my answer comes out to be sin (((3nθ)/(2 − n))) . Where is the mistake?](https://www.tinkutara.com/question/Q13665.png)
$$\mathrm{But}\:\mathrm{I}\:\mathrm{have}\:\mathrm{calculated}\:\mathrm{it}\:\mathrm{using}\:\mathrm{the}\:\mathrm{formula} \\ $$$${S}_{{n}} \:=\:\frac{\mathrm{sin}\frac{{n}\beta}{\mathrm{2}}}{\mathrm{sin}\frac{\beta}{\mathrm{2}}}\:\mathrm{sin}\left[\alpha\:+\:\left({n}\:−\:\mathrm{1}\right)\frac{\beta}{\mathrm{2}}\right] \\ $$$$\mathrm{where}\:\alpha\:\mathrm{is}\:\mathrm{the}\:\mathrm{first}\:\mathrm{angle}\:\mathrm{and}\:\beta\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{common}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{which} \\ $$$$\mathrm{are}\:\mathrm{in}\:\mathrm{AP}\:{i}.{e}.\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{sin}\alpha\:+ \\ $$$$\mathrm{sin}\left(\alpha\:+\:\beta\right)\:+\:\mathrm{sin}\left(\alpha\:+\:\mathrm{2}\beta\right)\:+\:…\:+ \\ $$$$\mathrm{sin}\left[\alpha\:+\:\left({n}\:−\:\mathrm{1}\right)\beta\right]. \\ $$$$\mathrm{Using}\:\alpha\:=\:\theta\:\mathrm{and}\:\frac{\beta}{\mathrm{2}}\:=\:\frac{\theta}{\mathrm{2}\:−\:{n}}\:,\:\mathrm{my}\:\mathrm{answer} \\ $$$$\mathrm{comes}\:\mathrm{out}\:\mathrm{to}\:\mathrm{be}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{n}\theta}{\mathrm{2}\:−\:{n}}\right)\:.\:\mathrm{Where} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{mistake}? \\ $$
Commented by ajfour last updated on 22/May/17
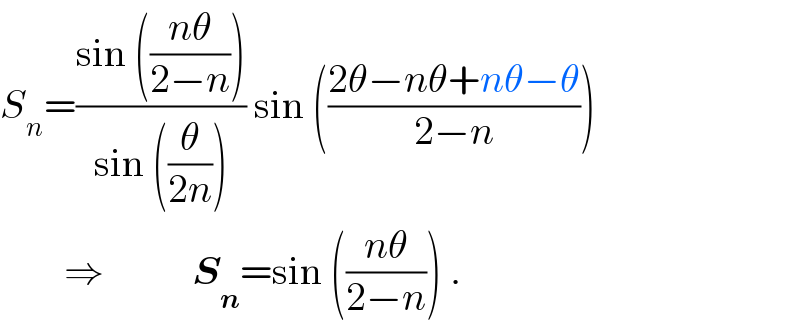
$${S}_{{n}} =\frac{\mathrm{sin}\:\left(\frac{{n}\theta}{\mathrm{2}−{n}}\right)}{\mathrm{sin}\:\left(\frac{\theta}{\mathrm{2}{n}}\right)}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\theta−{n}\theta+{n}\theta−\theta}{\mathrm{2}−{n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{S}}_{\boldsymbol{{n}}} =\mathrm{sin}\:\left(\frac{{n}\theta}{\mathrm{2}−{n}}\right)\:. \\ $$
Commented by Tinkutara last updated on 22/May/17
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{I}\:\mathrm{understood}. \\ $$
