Menu Close

The-sum-of-two-integers-is-304-and-their-GCD-is-19-What-are-the-numbers-

Tinku Tara 0 Comments
Pin




Question Number 104413 by Anindita last updated on 21/Jul/20
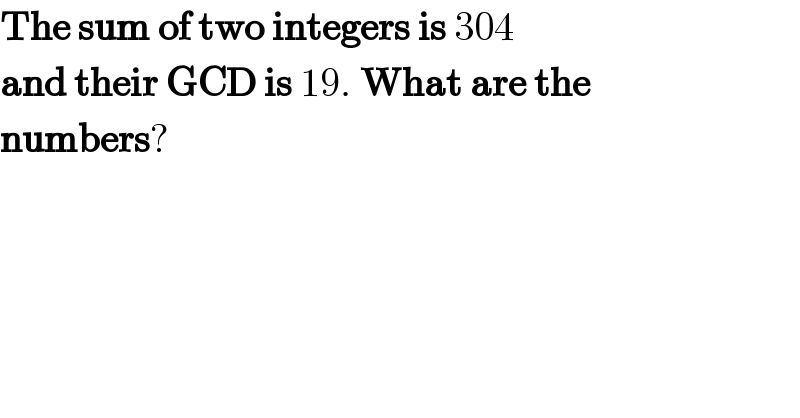
The sum of two integers is 304 and their GCD is 19. What are the numbers?
$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{two}}\:\boldsymbol{\mathrm{integers}}\:\boldsymbol{\mathrm{is}}\:\mathrm{304} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{their}}\:\boldsymbol{\mathrm{GCD}}\:\boldsymbol{\mathrm{is}}\:\mathrm{19}.\:\boldsymbol{\mathrm{What}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{numbers}}? \\ $$
Answered by Rasheed.Sindhi last updated on 22/Jul/20
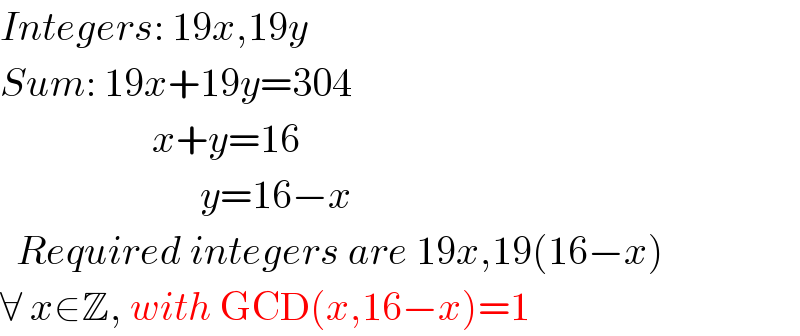
Integers: 19x,19y Sum: 19x+19y=304 x+y=16 y=16−x Required integers are 19x,19(16−x) ∀ x∈Z, with GCD(x,16−x)=1
$${Integers}:\:\mathrm{19}{x},\mathrm{19}{y} \\ $$$${Sum}:\:\mathrm{19}{x}+\mathrm{19}{y}=\mathrm{304} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}+{y}=\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{16}−{x} \\ $$$$\:\:{Required}\:{integers}\:{are}\:\mathrm{19}{x},\mathrm{19}\left(\mathrm{16}−{x}\right) \\ $$$$\forall\:{x}\in\mathbb{Z},\:{with}\:\mathrm{GCD}\left({x},\mathrm{16}−{x}\right)=\mathrm{1} \\ $$
Commented by floor(10²Eta[1]) last updated on 21/Jul/20
you are including all the cases when gcd(x, y)≠1 which is not correct
$$\mathrm{you}\:\mathrm{are}\:\mathrm{including}\:\mathrm{all}\:\mathrm{the}\:\mathrm{cases}\:\mathrm{when} \\ $$$$\mathrm{gcd}\left(\mathrm{x},\:\mathrm{y}\right)\neq\mathrm{1}\:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Jul/20
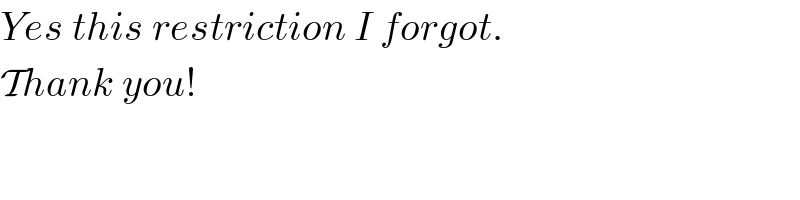
Yes this restriction I forgot. Thank you!
$${Yes}\:{this}\:{restriction}\:{I}\:{forgot}. \\ $$$$\mathcal{T}{hank}\:{you}! \\ $$
Answered by 1549442205PVT last updated on 21/Jul/20
Since GCD(a,b)=19 ⇒ { ((a=19m)),((b=19n)) :} where gcd(m,n)=1 From the hypothesis a+b=304 we get 19(m+n)=304⇒m+n=16. WLOG we suppose m<n.Then we have the following cases: (note that gcd(m,n)=1⇒m is odd) i)m=1⇒n=15⇒(a,b)=(19,285) ii)m=3⇒n=13⇒(a,b)=(57,247) iii)m=5⇒n=11⇒(a,b)=(209,95) iv)m=7⇒n=9⇒(a,b)=(153,151) Thus all the pairs (a,b) of positive integers which we need to find as: (a,b)∈{(19;285),(57,247),(209;95),(153;151)} and the permutations of them
$$\mathrm{Since}\:\mathrm{GCD}\left(\mathrm{a},\mathrm{b}\right)=\mathrm{19}\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{19m}}\\{\mathrm{b}=\mathrm{19n}}\end{cases} \\ $$$$\mathrm{where}\:\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{a}+\mathrm{b}=\mathrm{304}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{19}\left(\mathrm{m}+\mathrm{n}\right)=\mathrm{304}\Rightarrow\mathrm{m}+\mathrm{n}=\mathrm{16}. \\ $$$$\mathrm{WLOG}\:\mathrm{we}\:\mathrm{suppose}\:\mathrm{m}<\mathrm{n}.\mathrm{Then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{the}\:\mathrm{following}\:\mathrm{cases}: \\ $$$$\left(\mathrm{note}\:\mathrm{that}\:\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1}\Rightarrow\mathrm{m}\:\mathrm{is}\:\mathrm{odd}\right) \\ $$$$\left.\mathrm{i}\right)\mathrm{m}=\mathrm{1}\Rightarrow\mathrm{n}=\mathrm{15}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{19},\mathrm{285}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{m}=\mathrm{3}\Rightarrow\mathrm{n}=\mathrm{13}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{57},\mathrm{247}\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{m}=\mathrm{5}\Rightarrow\mathrm{n}=\mathrm{11}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{209},\mathrm{95}\right) \\ $$$$\left.\mathrm{iv}\right)\mathrm{m}=\mathrm{7}\Rightarrow\mathrm{n}=\mathrm{9}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{153},\mathrm{151}\right) \\ $$$$\mathrm{Thus}\:\mathrm{all}\:\mathrm{the}\:\mathrm{pairs}\:\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{which}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:\mathrm{as}: \\ $$$$\left(\mathrm{a},\mathrm{b}\right)\in\left\{\left(\mathrm{19};\mathrm{285}\right),\left(\mathrm{57},\mathrm{247}\right),\left(\mathrm{209};\mathrm{95}\right),\left(\mathrm{153};\mathrm{151}\right)\right\} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{permutations}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{them}} \\ $$$$ \\ $$
Commented by floor(10²Eta[1]) last updated on 21/Jul/20
gcd(153,151)=1≠19. the last case should be (a,b)=(133,171)
$$\mathrm{gcd}\left(\mathrm{153},\mathrm{151}\right)=\mathrm{1}\neq\mathrm{19}. \\ $$$$\mathrm{the}\:\mathrm{last}\:\mathrm{case}\:\mathrm{should}\:\mathrm{be} \\ $$$$\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{133},\mathrm{171}\right) \\ $$
Commented by floor(10²Eta[1]) last updated on 21/Jul/20
m=2s+1, n=2t+1 m+n=2s+2t+2=16⇒s+t=7 s=k, t=7−k m=2k+1, n=15−2k 2k+1<15−2k⇒k≤3 so all the pairs (a, b) of integers are: (a, b)={19(2k+1), 19(15−2k)} ∀ k≤3
$$\mathrm{m}=\mathrm{2s}+\mathrm{1},\:\mathrm{n}=\mathrm{2t}+\mathrm{1} \\ $$$$\mathrm{m}+\mathrm{n}=\mathrm{2s}+\mathrm{2t}+\mathrm{2}=\mathrm{16}\Rightarrow\mathrm{s}+\mathrm{t}=\mathrm{7} \\ $$$$\mathrm{s}=\mathrm{k},\:\mathrm{t}=\mathrm{7}−\mathrm{k} \\ $$$$\mathrm{m}=\mathrm{2k}+\mathrm{1},\:\mathrm{n}=\mathrm{15}−\mathrm{2k} \\ $$$$\mathrm{2k}+\mathrm{1}<\mathrm{15}−\mathrm{2k}\Rightarrow\mathrm{k}\leqslant\mathrm{3} \\ $$$$\mathrm{so}\:\mathrm{all}\:\mathrm{the}\:\mathrm{pairs}\:\left(\mathrm{a},\:\mathrm{b}\right)\:\mathrm{of}\:\mathrm{integers}\:\mathrm{are}: \\ $$$$\left(\mathrm{a},\:\mathrm{b}\right)=\left\{\mathrm{19}\left(\mathrm{2k}+\mathrm{1}\right),\:\mathrm{19}\left(\mathrm{15}−\mathrm{2k}\right)\right\}\:\forall\:\mathrm{k}\leqslant\mathrm{3} \\ $$$$ \\ $$
Commented by 1549442205PVT last updated on 22/Jul/20
Thank you sir,i mistaked this case
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\mathrm{i}\:\mathrm{mistaked}\:\mathrm{this}\:\mathrm{case} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *