Question Number 20671 by Tinkutara last updated on 31/Aug/17
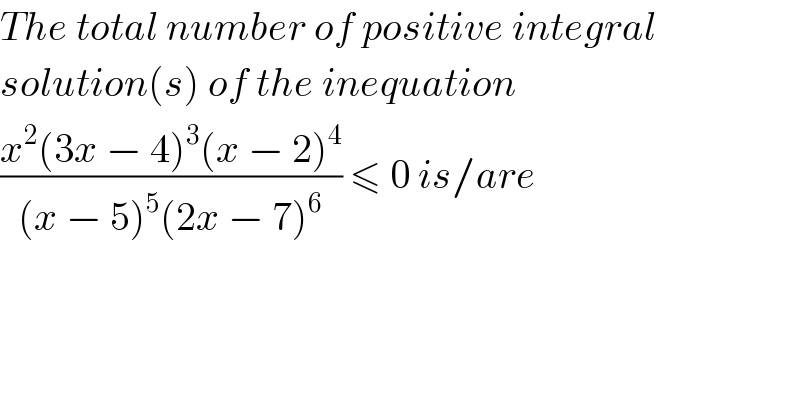
$${The}\:{total}\:{number}\:{of}\:{positive}\:{integral} \\ $$$${solution}\left({s}\right)\:{of}\:{the}\:{inequation} \\ $$$$\frac{{x}^{\mathrm{2}} \left(\mathrm{3}{x}\:−\:\mathrm{4}\right)^{\mathrm{3}} \left({x}\:−\:\mathrm{2}\right)^{\mathrm{4}} }{\left({x}\:−\:\mathrm{5}\right)^{\mathrm{5}} \left(\mathrm{2}{x}\:−\:\mathrm{7}\right)^{\mathrm{6}} }\:\leqslant\:\mathrm{0}\:{is}/{are} \\ $$
Answered by ajfour last updated on 31/Aug/17

$${four} \\ $$$${x}=\mathrm{0},\:\:\mathrm{2},\:\mathrm{3},\:\mathrm{4} \\ $$
Commented by Tinkutara last updated on 31/Aug/17

$$\mathrm{But}\:\mathrm{integral}\:\mathrm{values}\:\mathrm{are}\:\mathrm{to}\:\mathrm{be}\:\mathrm{counted}. \\ $$$$\mathrm{So}\:\mathrm{it}\:\mathrm{is}\:\mathrm{4}.\:\mathrm{Thank}\:\mathrm{you}! \\ $$
Commented by ajfour last updated on 01/Sep/17

