Question Number 17096 by Tinkutara last updated on 30/Jun/17
![The total number of solutions of the equation tan 3x − tan 2x − tan 3x tan 2x = 1 in [0, 2π] is](https://www.tinkutara.com/question/Q17096.png)
$$\mathrm{The}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation} \\ $$$$\mathrm{tan}\:\mathrm{3}{x}\:−\:\mathrm{tan}\:\mathrm{2}{x}\:−\:\mathrm{tan}\:\mathrm{3}{x}\:\mathrm{tan}\:\mathrm{2}{x}\:=\:\mathrm{1}\:\mathrm{in} \\ $$$$\left[\mathrm{0},\:\mathrm{2}\pi\right]\:\mathrm{is} \\ $$
Answered by sma3l2996 last updated on 30/Jun/17
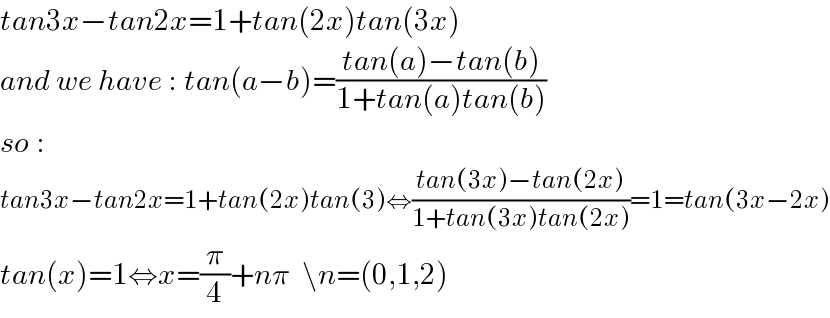
$${tan}\mathrm{3}{x}−{tan}\mathrm{2}{x}=\mathrm{1}+{tan}\left(\mathrm{2}{x}\right){tan}\left(\mathrm{3}{x}\right) \\ $$$${and}\:{we}\:{have}\::\:{tan}\left({a}−{b}\right)=\frac{{tan}\left({a}\right)−{tan}\left({b}\right)}{\mathrm{1}+{tan}\left({a}\right){tan}\left({b}\right)} \\ $$$${so}\:: \\ $$$${tan}\mathrm{3}{x}−{tan}\mathrm{2}{x}=\mathrm{1}+{tan}\left(\mathrm{2}{x}\right){tan}\left(\mathrm{3}\right)\Leftrightarrow\frac{{tan}\left(\mathrm{3}{x}\right)−{tan}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{tan}\left(\mathrm{3}{x}\right){tan}\left(\mathrm{2}{x}\right)}=\mathrm{1}={tan}\left(\mathrm{3}{x}−\mathrm{2}{x}\right) \\ $$$${tan}\left({x}\right)=\mathrm{1}\Leftrightarrow{x}=\frac{\pi}{\mathrm{4}}+{n}\pi\:\:\backslash{n}=\left(\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$
Commented by Tinkutara last updated on 30/Jun/17

$$\mathrm{But}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0}. \\ $$
Commented by prakash jain last updated on 30/Jun/17

$$\mathrm{may}\:\mathrm{be}\:\mathrm{because}\:\mathrm{solution}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{satisfy}\:\mathrm{original}\:\mathrm{equation}. \\ $$
Commented by mrW1 last updated on 30/Jun/17
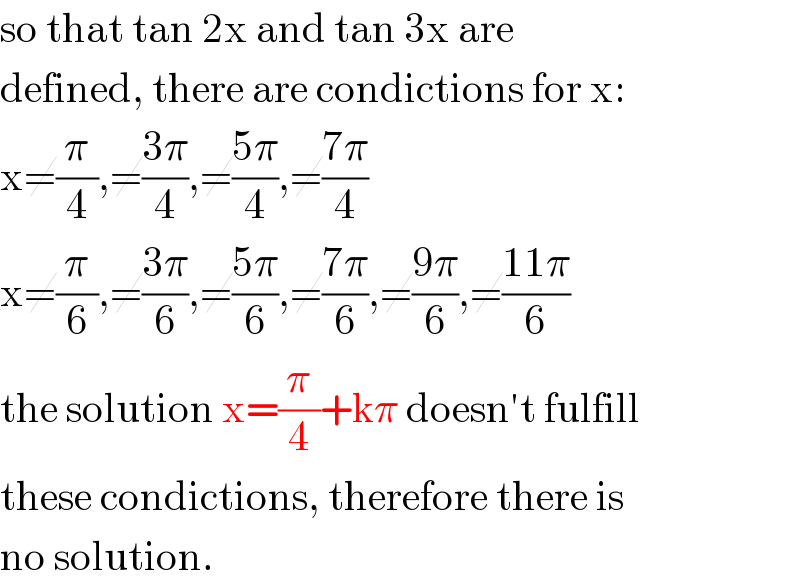
$$\mathrm{so}\:\mathrm{that}\:\mathrm{tan}\:\mathrm{2x}\:\mathrm{and}\:\mathrm{tan}\:\mathrm{3x}\:\mathrm{are} \\ $$$$\mathrm{defined},\:\mathrm{there}\:\mathrm{are}\:\mathrm{condictions}\:\mathrm{for}\:\mathrm{x}: \\ $$$$\mathrm{x}\neq\frac{\pi}{\mathrm{4}},\neq\frac{\mathrm{3}\pi}{\mathrm{4}},\neq\frac{\mathrm{5}\pi}{\mathrm{4}},\neq\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$$\mathrm{x}\neq\frac{\pi}{\mathrm{6}},\neq\frac{\mathrm{3}\pi}{\mathrm{6}},\neq\frac{\mathrm{5}\pi}{\mathrm{6}},\neq\frac{\mathrm{7}\pi}{\mathrm{6}},\neq\frac{\mathrm{9}\pi}{\mathrm{6}},\neq\frac{\mathrm{11}\pi}{\mathrm{6}} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{x}=\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\:\mathrm{doesn}'\mathrm{t}\:\mathrm{fulfill} \\ $$$$\mathrm{these}\:\mathrm{condictions},\:\mathrm{therefore}\:\mathrm{there}\:\mathrm{is} \\ $$$$\mathrm{no}\:\mathrm{solution}. \\ $$
Commented by mrW1 last updated on 30/Jun/17
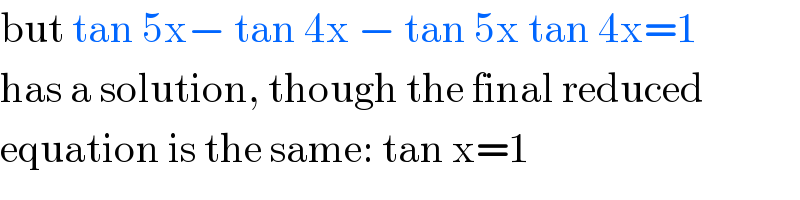
$$\mathrm{but}\:\mathrm{tan}\:\mathrm{5x}−\:\mathrm{tan}\:\mathrm{4x}\:−\:\mathrm{tan}\:\mathrm{5x}\:\mathrm{tan}\:\mathrm{4x}=\mathrm{1} \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{solution},\:\mathrm{though}\:\mathrm{the}\:\mathrm{final}\:\mathrm{reduced} \\ $$$$\mathrm{equation}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}:\:\mathrm{tan}\:\mathrm{x}=\mathrm{1} \\ $$
Commented by Tinkutara last updated on 01/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sirs}! \\ $$
